A plane loop, shaped as two squares of sides a=1m and b=0.4 m is introduced into a uniform magnetic field perpendicular to the pane of loop. The manetic field varies as B=10−3sin(100)T. The amplitude of the current (in A) induced in the loop is its resistance per unit length is r=5mΩm−1 is

ϕ (flux linked) =a2Bcos0∘−b2Bcos180∘
E=−dϕdt=−(a2−b2)dBdt=(a2−b2)B0ωcosωt
where B=B0sinωt,B0=10−3T,ω=100
∴Imax=(a2−b2)B0ωR
and R=(4a+4b)r=4(a+b)r
∴Imax=(a−b)B0ω4r=(1−0.4)×10−3×1004×5×10−3=3A
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -21 : (ALTERNATING CURRENT)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 22 : (ELECTROMAGNETIC WAVES)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 19 : (MAGNETISM AND MATTER)14videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
ATOMS
- BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator30videos
COMMUNICATION SYSTEM
Similar Questions
A plane loop, shaped as two squares of sides a=1m and b=0.4m is introduced into a uniform magnetic field ⊥ to the plane of loop . The magnetic field varies as B=10(−3)sin(100t)T. The qamplitude of the current induced in the loop if its resistance per unit length is r=5mΩm−1 is
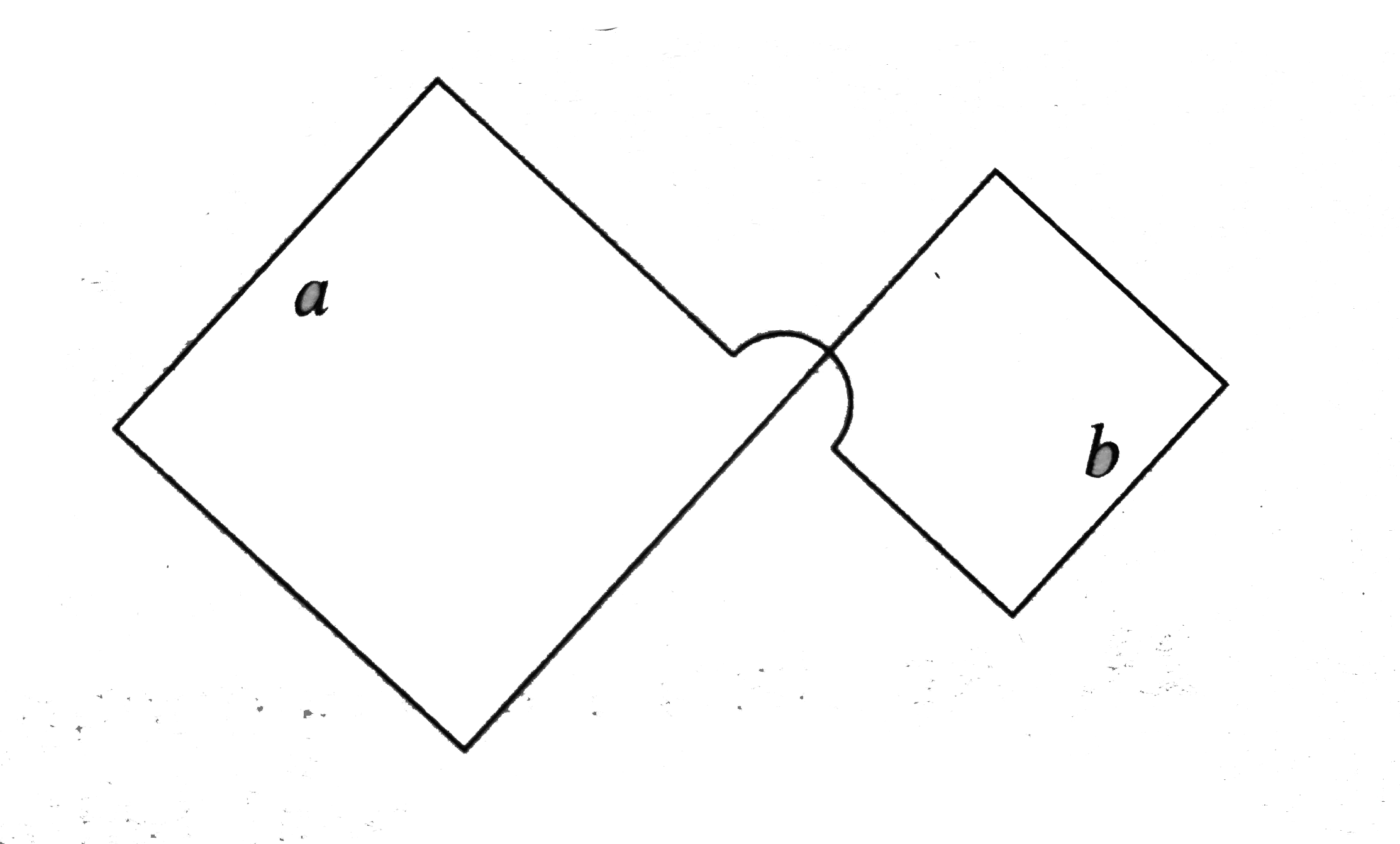 View Solution
View SolutionA plane loop shown in figure-5.71 is shaped in the from of two squares with sides a and b and it is introduced into a uniform magnetic field at right angles, to the loop's plane. The magnetic induction varies with time as B=B0sinωt. find the amplitude of the current induced in the loop if its resistance per unit length is equal to r. the induction of the loop is negligible.
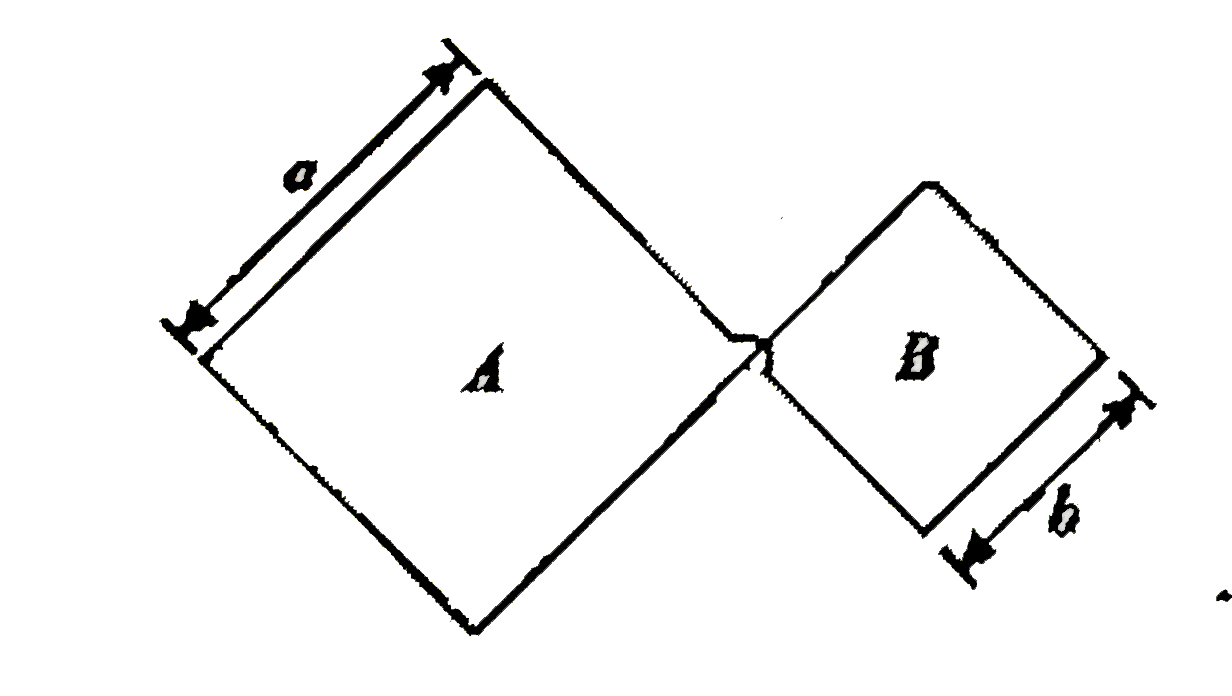 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A plane loop, shaped as two squares of sides a=1m and b=0.4m is introduced into a uniform magnetic field ⊥ to the plane of loop . The magnetic field varies as B=10(−3)sin(100t)T. The qamplitude of the current induced in the loop if its resistance per unit length is r=5mΩm−1 is
 A(a) 2AB(b) 3AC( c) 4AD(d) 5A
A(a) 2AB(b) 3AC( c) 4AD(d) 5A - Question 2 - Select One
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero - Question 3 - Select One
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
 A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 View Solution
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
View SolutionA plane loop is shaped ion the from as shown in the figure with radii a and b and is placed in a uniform time varying magnetic field B=B0sinωt . Find the amplitude of the current induced in the loop if its resistance per unit length is equal to λ . The inductance of the loop negligible.
 View Solution
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
View Solutiona conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is
 View Solution
View Solution
