The magnetic field perpendicular to the plane of a loop of area is 0.2 T. Calculate the magnetic flux through the loop (in weber)
0.01
0.02
0.03
0.04
The correct Answer is:B
To calculate the magnetic flux through the loop, we can follow these steps:
1. Identify the Given Values:
- Area of the loop (A) = 0.1 m²
- Magnetic field (B) = 0.2 T
- Angle (θ) between the magnetic field and the area vector = 0° (since the magnetic field is perpendicular to the loop)
2. Recall the Formula for Magnetic Flux:
The magnetic flux (Φ) through a surface is given by the formula:
Φ=B⋅A⋅cos(θ)
3. Substitute the Values into the Formula:
Since the angle θ is 0°, we know that:
cos(0°)=1
Therefore, we can substitute the values into the formula:
Φ = 0.2 \, \text{T} \cdot 0.1 \, \text{m}² \cdot \cos(0°)
Φ=0.2T⋅0.1m²⋅1
4. Calculate the Magnetic Flux:
Now, perform the multiplication:
Φ=0.2⋅0.1=0.02Weber
5. Final Result:
The magnetic flux through the loop is:
Φ=0.02Weber
- Area of the loop (A) = 0.1 m²
- Magnetic field (B) = 0.2 T
- Angle (θ) between the magnetic field and the area vector = 0° (since the magnetic field is perpendicular to the loop)
The magnetic flux (Φ) through a surface is given by the formula:
Φ=B⋅A⋅cos(θ)
Since the angle θ is 0°, we know that:
cos(0°)=1
Therefore, we can substitute the values into the formula:
Φ = 0.2 \, \text{T} \cdot 0.1 \, \text{m}² \cdot \cos(0°)
Φ=0.2T⋅0.1m²⋅1
Now, perform the multiplication:
Φ=0.2⋅0.1=0.02Weber
The magnetic flux through the loop is:
Φ=0.02Weber
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-B
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 5
5 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
Assertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
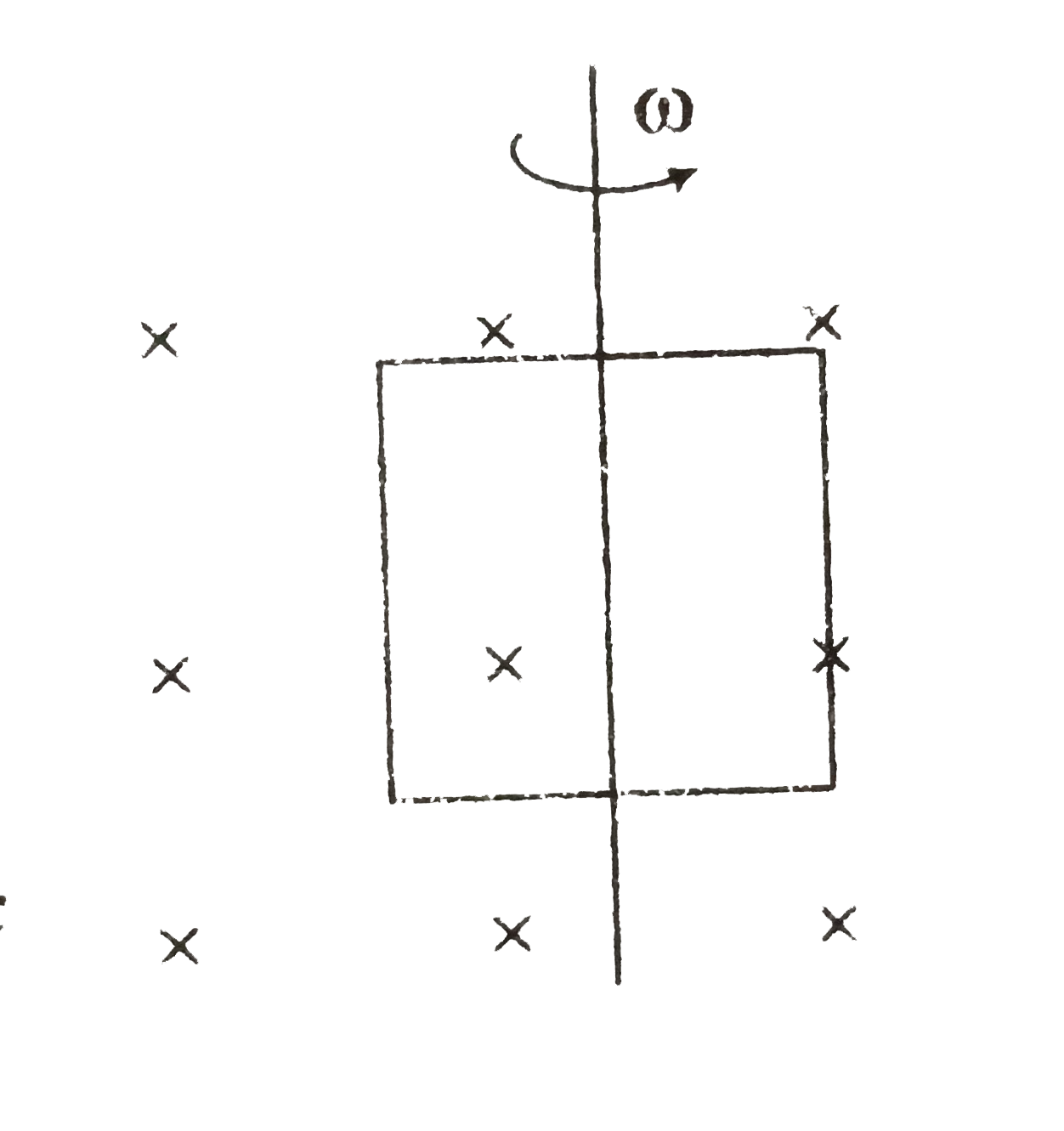
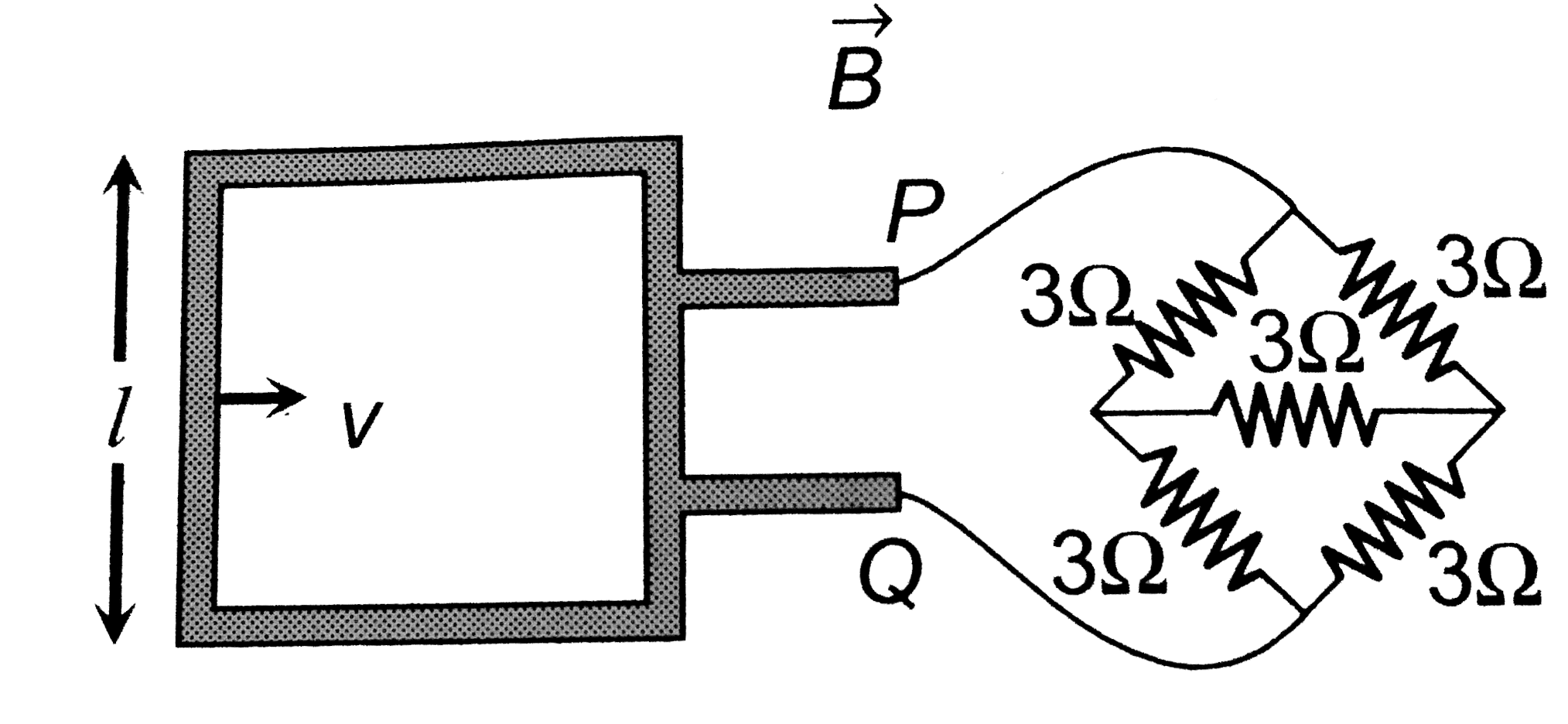
View SolutionA square metallic wire loop of side 0.1 m and resistance of 1Ω is moved with a constant velocity in a magnetic field of 2wb/m2 as shown in figure. The magnetic field field is perpendicular to the plane of the loop, loop is coonected to a network of resistances. what should be the velocity of loop so as to have a steady current of 1mA in loop?
View Solution
Knowledge Check
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
A(BA)2μ0πBBA√Aμ0CBA√Aμ0πD2BA√Aμ0√πA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A square metal wire loop of side 10cm and resistances 1Ω is moved with constant velocity v0 in a uniform magnetic field of induction B=2Wbm−2, as shown in Fig. 3.218. The magnetic field lines are perpendicular to the plane of loop network of resistances, each of value 3Ω. The speed of the loop so as to have a steady current of 1mA in the loop is

View SolutionA loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionMagnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionA square metal wire loop of side 20 cm and resistance 2Ω is moved with a constant velcoity v0 in a uniform magnetic field of induction B = 1 Wb/m2 as shown in the figure. The magnetic field lines are perpendicular to the plane of the loop. The loop is connected to a network of resistance each of value 5Ω. The resistances of the lead wires BF and AE are negligible. What should be the speed of the loop, so as to have a steady current of 2 mA in the loop? Give the direction of current in the loop.

View Solution
