A concave mirror has radius of curvature of 40 cm. It is at the bottom of a glass that has water filled up to 5 m. If a small particle is floating on the surface of water, its image as seen, from directly above the glass, is at a distance d from the surface of water. The value of d (in cm) is:
(Refractive index of water =1.33)

If v is the distance of image formed by mirror, then
1v+1u=1f
or 1v+1−5=1−20
∴v=203 cm
Distance of this image from water surface
=203+5=353cm
using RDAD=μ
∴AD=d=RDμ=(35/3)1.33=8.8cm
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 24 : (WAVE OPTICS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -25 : (DUAL NATURE OF RADIATION AND MATTER)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 22 : (ELECTROMAGNETIC WAVES)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
A concave mirror of radius of curvature one meter is placed at the bottom of a tank of water. The mirror forms an image of the sun when it is directly overhead. Calculate the distance of the images from the mirror for (a) 80cm and (b) 40cm of water in the tank ( μ=4/3 for water)
View SolutionA concave mirror of radius 40 cm lies on a horizontal table and water is filled in it upto a height of 5.00 cm. A small dust particle floats on the water surface at a point P vertically above the point of contact of the mirror with the table. Locate the image of the dust particle as seen from a point directly above it. the refractive index of water is 1.33.
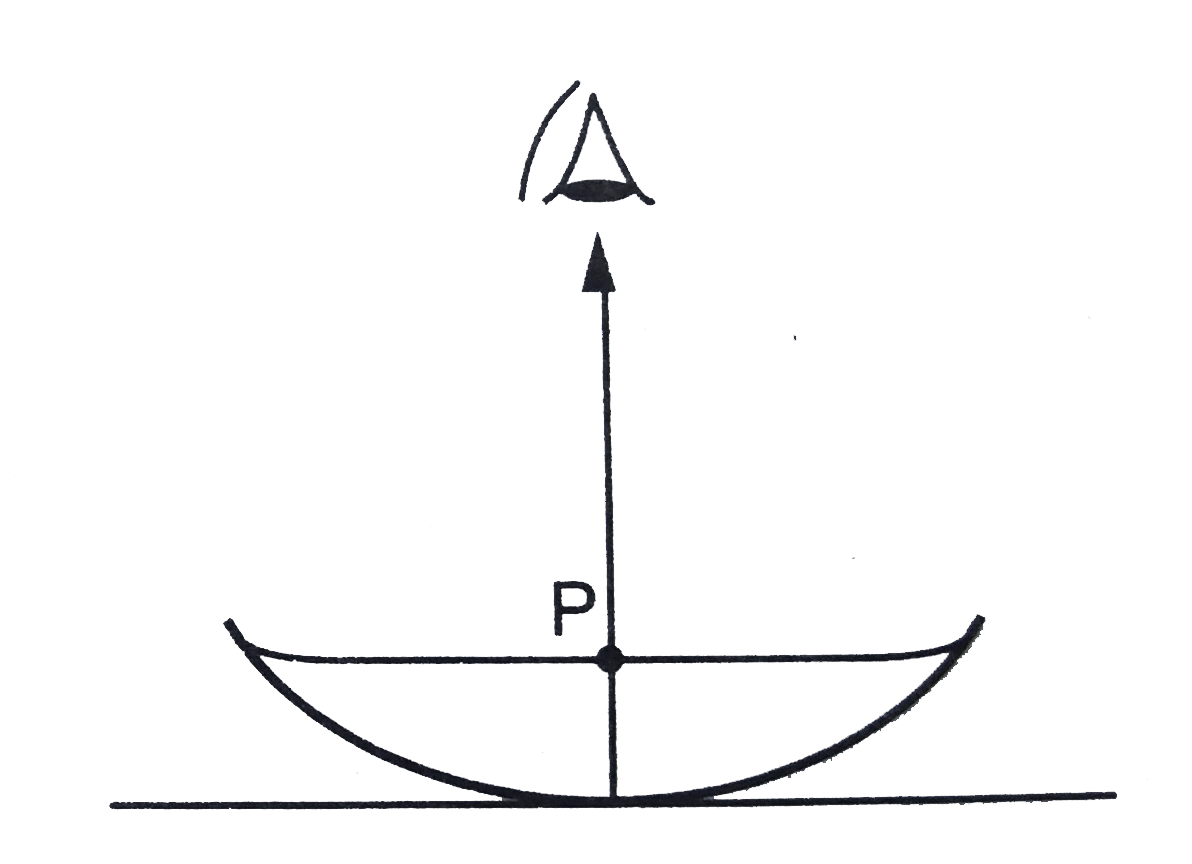
View Solution
Knowledge Check
A glass beaker is filled with water up to 5cm. It is kept on top of a 2cm thick glass slab. When a coin at the bottom of the glass slab is viewed at the normal incidence from above the beaker, its apparent depth from the water surface is dcm. Value of d is close (the refractive index of water and glass are 1.33 and 1.50,respectively)
A2.5B5.1C3.7D6
A concave mirror of radius 40 cm lies on a horizontla tale and wateis filled in it up t a heightof 5.00 cm. A small dust particle floats on the water surface at a point P vertically above tge pointof contact of the miror with the table. Locate the image of the dust particle as seen from a point directly above it. tEh refractie index of water is 1.33.

View SolutionA concave mirror of radius 40 cm lies on a horizontla tale and wateis filled in it up t a heightof 5.00 cm. A small dust particle floats on the water surface at a point P vertically above tge pointof contact of the miror with the table. Locate the image of the dust particle as seen from a point directly above it. tEh refractie index of water is 1.33.

View SolutionA concave mirror of radius 40 cm lies on a horizontla tale and wateis filled in it up t a heightof 5.00 cm. A small dust particle floats on the water surface at a point P vertically above tge pointof contact of the miror with the table. Locate the image of the dust particle as seen from a point directly above it. tEh refractie index of water is 1.33.

View SolutionIf the refractive index from air to glass is 1.5 ,and the refractive index of water is 1.33. What is the refractive index from glass into water?
View SolutionAt the bottom of a trough filled with water a rectangular glass slab is placed. A ray of light is incident on the water surface at an angle of 30∘ and enters the glass after passing through the water. What is the angle of refraction in glass? Given, refractive index of water is 1.33 and that of glass is 1.5.
View SolutionA thin walled glass sphere of radius 2.5 cm is filled with water. An object (O) is placed at 7.5 cm from the effect of glass wall, at what distance the image (I) of the object , measured from the centre of sphere is formed ? (refractive index of water = 1.333)

View SolutionA thin walled glass sphere of radius 2.5 cm is filled with water. An object (O) is placed at 7.5 cm from the effect of glass wall, at what distance the image (I) of the object , measured from the centre of sphere is formed ? (refractive index of water = 1.333)

View Solution
