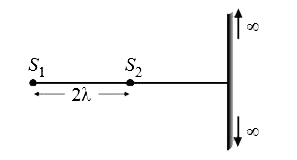
There are two sources kept at distance 2λ. A large screen is perpendicular to line joining the sources. Number of maximas on the screen in this case is (λ= wavelength of light)

Δxmax=0 and Δxmax=2λ
The Theortical maximas are =2n+1=2×1+1=5
But on the screen there wil be three maximas.
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -25 : (DUAL NATURE OF RADIATION AND MATTER)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 26 : (ATOMS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 23 : (RAY OPTICS AND OPTICAL INSTRUMENTS)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
The two coherent sources of monochromatic light of wavelength λ are located at a separation λ. The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
View SolutionA monochromatic point source(S1) is at a distance d from a screen. Another identical source (S2) is at a large distance from the screen. The two sources are on a line which is perpendicular to the screen. Sources are coherent. What is the shape of interference fringes on the screen?
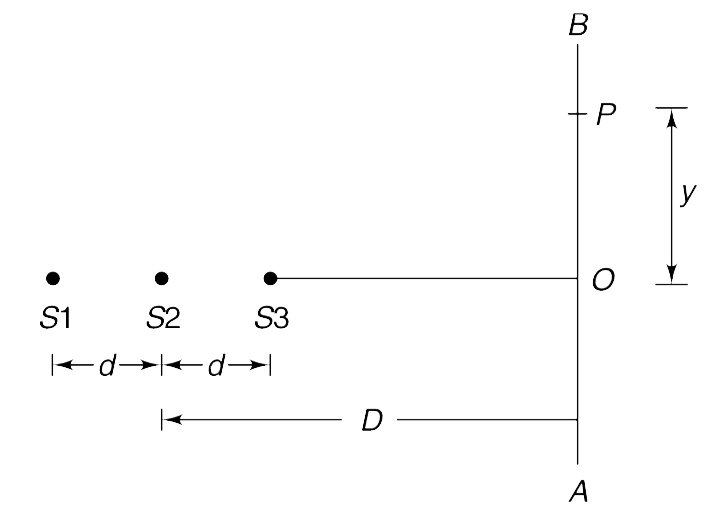
(b) Three identical coherent sources are placed on a straight line with two neighbouring ones separated by a distance d = 0.06 mm. The sources produce monochromatic light of wavelength λ = 550.4 nm. A line AB is located at a distance D = 2.50 m from the sources and is perpendicular to line joining the three sources. Intensity of light at P with any one of the sources switched on is Io. Find the intensity when all three sources are switched on. Distance of point P from O isy = 1.72 cm (see figure)
View Solution
Knowledge Check
There are two sources kept at distances 2λ. A large screen is perpendicular to line joining the sources. Number of maximas on the screen in this case is (λ=wavelength of light)
 A1B3C5D7
A1B3C5D7The distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
A4000ÅB5000ÅC6000ÅD7200ÅThe distance of a point on a screen from two coherent light sources differs by 93 wavelengths. If the path difference is 0.0465 mm, then the wavelength of light used is
A4000 ÅB4500 ÅC5000 ÅD7500 Å
The distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
View SolutionTwo point sources oscillating in the same phase are on a straight line perpendicular to a screen. The nearest source is at a distance of D » λ from the screen. What shape will the interference fringes have on the screen? What is the distance on the screen from the perpendicular to the nearest bright fringe if the distance between the sources is l=nλ (n is an integer)? Note that λ « l.
View SolutionThe figure shows two points source which emit light of wavelength λ in phase with each other and are at a distance d=5.5λ apart along a line which is perpendicular to a large screen at a distance L from the centre of the source. Assume that d is much less than L. Which of the following statement is (are) correct ?
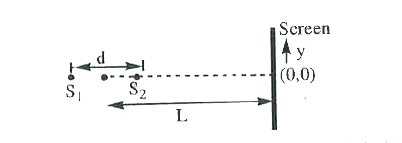
View SolutionTwo point sources are d=nλ apart. A screen is held at right angles to the line joining the two sources at a distance D from the nearer source. Calculate the distance of the point on the screen where the first bright fringe is observed. Assume D>>d.
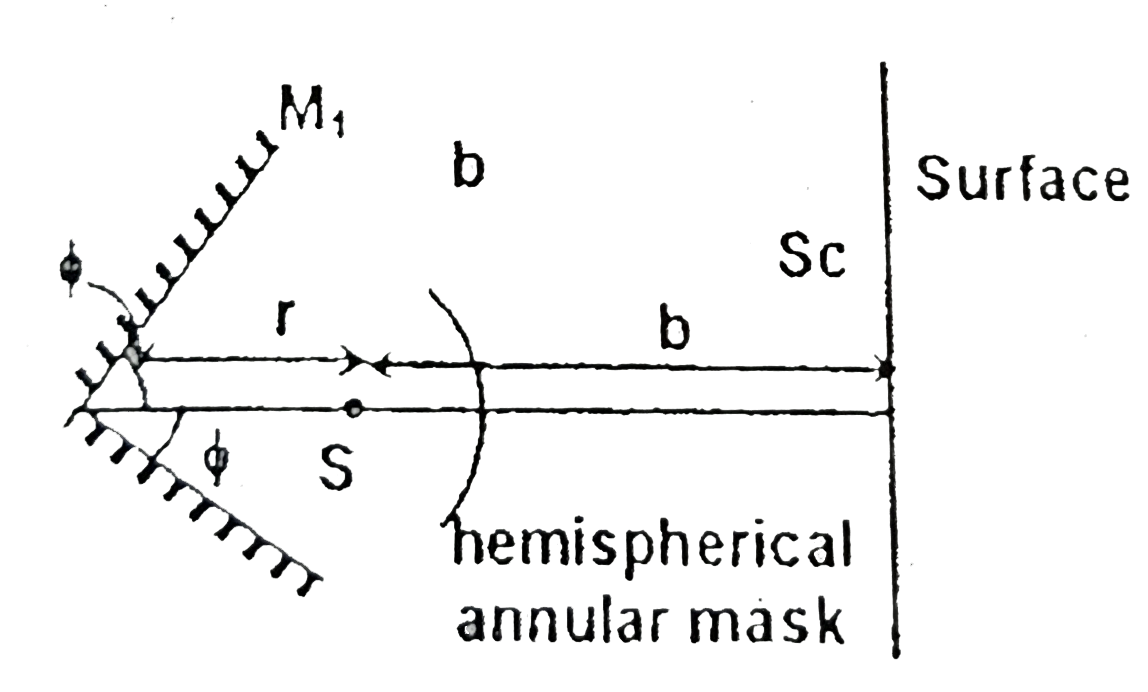
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
View Solution
