निचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनुरूपी निर्देश वृत्त का आरेखा खीचिए घूर्णी कण की आरंभिक (t=0) स्थिति वृत्त की त्रिज्या तथा कोणीय चाल दर्शाइए। सगमता के लिए प्रत्येक प्रकरण में परिक्रमण की दिशा वामावर्त कीजिए (x को cm में तथा t को s में लीजिए )।
(a)x=−sin(3t+π3)
(b) x=cos(π6−t)
(c)x=2sin(2πt+π4)
(d)x=2cosπt
(a ) दिया गया समीकरण है =−2sin(3t+π3)
=2cos(π2+3t+π3)
या x=2cos(3t+5π6) सेमी
समीकरण की x=Acos(ωt+ϕ) से तुलन करने पर
आयाम A=2 सेमी ω,=3 रेडियन/से प्रारंभिक कला कोण ϕ=5π6
तहा आवर्तकाल T=2πω=2π3 से
अतः दी गई समीकरण से निम्न वृत्त आरेख के द्वारा व्यक्त कर सकते है।
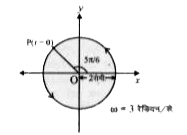
(b) दी गई समीकरण x=cos(π6−t) सेमी
x=cos(t−π6)∵cos(−θ)=cosθ
अतः समीकरण की x=A(ωt+ϕ) से तुलना करने पर
आयाम A=1सेमी ω=1 रेडियन/से, T=2πω=2π से ,
ϕ=−π6 अतः दी गई समीकरण निम्न वृत्त आरेख के द्वारा व्यक्त कर सकते है।
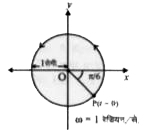
(c) दी गई समीकरण
x=3sin(2πt+π4) समी
x=3cos(3π2+2πt+π4)
=3cos(2πt+7π4)
x=Acos(ωt+ϕ) समी
समीकरण A=3 सेमी ω=2π,T=2πω1 से ϕ=7π4
अतः दी गई समीकरण निम्न वृत्त आरेख के द्वारा व्यक्त कर सकते है।
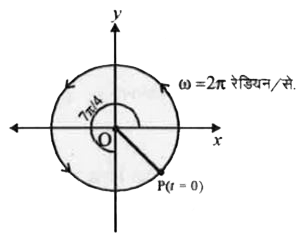
(d) दी गई समीकरण है -
x=2cos(πt)=cos(πt+0)समी
समीकरण की x=Acos(ωt+ϕ) से तुलन करने पर
आयाम A=2 सेमी ω=π रेडियन/से T=2πω=2 ϕ=0
अतः दी गई समीकरण वृत्त आरेख के द्वारा व्यक्त कर सकते है।
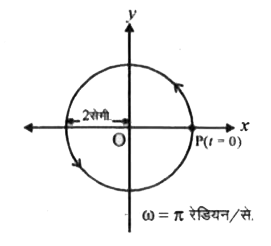
Topper's Solved these Questions
- दोलन BOOK - SCIENCE PUBLICATIONCHAPTER - दोलन EXERCISE - अन्य महत्त्वपूर्ण प्रश्न
14 Videos
- दोलन BOOK - SCIENCE PUBLICATIONCHAPTER - दोलन EXERCISE - अन्य महत्त्वपूर्ण प्रश्न -निबन्धात्मक प्रश्न
6 Videos
- दोलन BOOK - SCIENCE PUBLICATIONCHAPTER - दोलन EXERCISE - बोधात्मक प्रश्न
18 Videos
- तरलो के यांत्रिकी गुणBOOK - SCIENCE PUBLICATIONCHAPTER - तरलो के यांत्रिकी गुणEXERCISE - अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न )
24 Videos
- द्रव्य के तापीय गुणBOOK - SCIENCE PUBLICATIONCHAPTER - द्रव्य के तापीय गुणEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
23 Videos
Similar Questions
वृत्ताकार चाप पर कण को इसकी साम्यावस्था से अल्प कोणीय विस्थापन देने के कारण उत्पन्न गति के अभिलक्षण बताइये। इसका अवकल समीकरण भी लिखिये।
View Solutionसरल आवर्त गति के कण की स्थितिज ऊर्जा, गतिज ऊर्जा एवं कुल ऊर्जा के व्यंजक प्राप्त कर यांत्रिक ऊर्जा संरक्षण की पुष्टि कीजिये।
View Solutionएक लड़की झूले पर झूल रही है। यदि एक अन्य लड़की इसके साथ बैठ जाती है तो आवर्तकाल पर क्या प्रभाव होगा?
View Solutionएक वर्गाकार चकती (प्रत्येक भुजा 0.1m) किसी दूसरी समान्तर चकती पर 0.1m/s वेग से फिसल सकती है। दोनों प्लेटों को जल में डुबोया जाता है। यदि श्यानता गुणांक 0.01 प्वॉइज व श्यान बल 0.002N हो तो प्लेटों के मध्य दूरी (m) ज्ञात कीजिए |
View Solutionएक वस्तु का तापक्रम केल्विन पैमानों पर xK पाया जाता है। जब इसे फोरेहनाइट थर्मामीटर से मापा जाता है तो यह मान x∘F प्राप्त होता है तो x का मान ज्ञात कीजिए।
View Solutionरेखाओ y=mx+c तथाxa+yb=1 को xcosα+ysinα=p के रूप में लिखिए की लंब की लम्बाई ज्ञात कीजिये ।
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
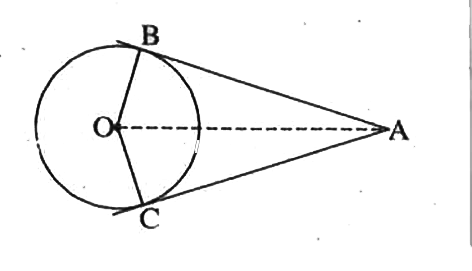
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
View Solutionबिंदुओं P और Q के निर्देशांक निम्नानुसार है:
P(5,−7),Q(−3,2)
प्रत्येक स्थिति में सदिश ¯¯¯¯¯¯PQ को एकांक सदिशों ¯i और ¯j के पदों में व्यक्त कीजिए तथा ∣∣¯¯¯¯¯¯PQ∣∣ की गणना कीजिए।
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionदोलन|सरल आवर्त गति #!#सरल आवर्त गति में त्वरण तथा आवर्तकाल का व्यंजक
View Solutionनिम्नलिखित संख्याओं में से प्रत्येक को अभाज्य गुणनखंडो की घातों के गुणनफल के रूप में व्यक्त कीजिए -
5400
View Solutionनिम्नलिखित संख्याओं में से प्रत्येक को अभाज्य गुणनखंडो की घातों के गुणनफल के रूप में व्यक्त कीजिए -
8575
View Solutionनिम्नलिखित संख्याओं में से प्रत्येक को अभाज्य गुणनखंडो की घातों के गुणनफल के रूप में व्यक्त कीजिए -
34300
View SolutionLi^(2+) की द्वितीय बोर कक्षा की त्रिज्या (बोर त्रिज्या (a_(0)) के पदों में) (xa_(0))/(y) द्वारा दी जातिही | जहाँ x+y का योग ज्ञात कीजिए -
View Solution
