Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g and 200g respectively. Each side of the equilateral triangle is 0.5 m long, 100g mass is at origin and 150g mass is on the X-axis.Solution in Telugu
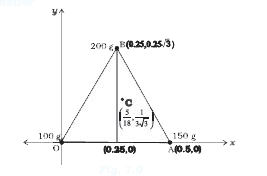
With the x–and y–axes chosen as shown in Fig. 7.9, the coordinates of points O, A and B forming the equilateral triangle are respectively (0,0), (0.5,0), (0.25,0.25√3). Let the masses 100 g, 150g and 200g be located at O, A and B be respectively. Then,
X=m1x1+m2x2+m3x3m1+m2+m3
=100(0)+150(0.5)+200(0.25)gm(100+150+200)g
=75+50450m=125450m=518m
Y=100(0)+150(0)+200(0.25√3)gm450g
=50√3450m=√39m=13√3m
The centre of mass C is shown in the figure. Note that it is not the geometric centre of the triangle OAB. Why?
Topper's Solved these Questions
- BOOK - NCERT TELUGUCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES29videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NCERT TELUGUCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)5videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NCERT TELUGUCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT TELUGUCHAPTER - THERMAL PROPERTIME OF MATTEREXERCISE - EXERCISES30videos
THERMAL PROPERTIME OF MATTER
Similar Questions
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?
04:50View SolutionDuring rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
09:19View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 01:24View Solution
01:24View SolutionThe triple points of neon and carbon dioxide are 24.57K and 216.55K respectively. Express these temperatures on the Celsius and Fahrenheit scales.
09:19View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png) 05:21View Solution
05:21View SolutionFind the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are 100g, 150 g, and 200g respectively. Each side of the equilateral triangle is 0.5m along.
05:59View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionFind the centre of mass of three paritcles at the vertices of an equilateral triangle. The masses of the particles are 100 g. 150g and 200 g respectively. Each side of the equilateral triangle is 0.5 m long.
06:41View SolutionFind the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g and 200g respectively. Each side of the equilateral triangle is 0.5 m long, 100g mass is at origin and 150g mass is on the X-axis.
02:42View Solutionएक समबाहु त्रिभुज के शीर्षों पर रखे गये तीन कणों का द्रव्यमान केंद्र ज्ञात कीजिए । कणों के द्रव्यमान क्रमश : 100g, 150g एवं 200 g हैं । त्रिभुज की प्रत्येक भुजा की लम्बाई 0.5 m है ।
05:58View SolutionFind the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
02:37View SolutionFind the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
05:05View SolutionFind the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
02:42View SolutionFind the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are 100g,150g,and200g respectively. Each side of the equilateral triangle is 0.5m along.
01:12View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png) View Solution
View SolutionThree particles A(50g), B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
View Solution

