Find the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.Solution in Telugu
Choosing the X and Y axes as shown in Fig. 7.11 we have the coordinates of the vertices of the L-shaped lamina as given in the figure. We can think of the L-shape to consist of 3 squares each of length 1m. The mass of each square is 1kg, since the lamina is uniform. The centres of mass of the squares are, by symmetry, their geometric centres and have coordinates (1/2,1/2), (3/2,1/2), (1/2,3/2) respectively. We take the masses of the squares to be concentrated at these points. The centre of mass of the whole L shape (X, Y) is the centre of mass of these mass points.
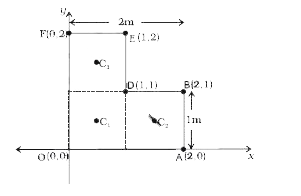
Hence
The centre of mass of the L-shape lies on the line OD. We could have guessed this without calculations. Can you tell why? Suppose, the three squares that make up the L shaped lamina of Fig. 7.11 had different masses. How will you then determine the centre of mass of the lamina?
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT TELUGUCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES
29 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT TELUGUCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
5 Videos
- OSCILLATIONSBOOK - NCERT TELUGUCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- THERMAL PROPERTIME OF MATTERBOOK - NCERT TELUGUCHAPTER - THERMAL PROPERTIME OF MATTEREXERCISE - EXERCISES
30 Videos
Similar Questions
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?
View SolutionDuring rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

View SolutionThe triple points of neon and carbon dioxide are 24.57K and 216.55K respectively. Express these temperatures on the Celsius and Fahrenheit scales.
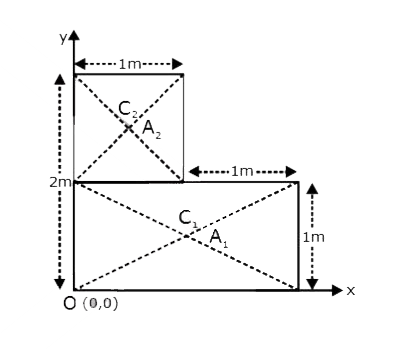
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
View SolutionFind the centre of mass of as uniform L -shaped lamina (a thin flast plate) with dimensions as shown in figure. The mass of lamina is 3 kg .
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.

View SolutionFind the centre of mass of a uniform I - shaped lamina (a thin flat plate) with dimensions as shown in figure. The mass of lamina is 3 kg
View SolutionThe x, y coordinates of the centre of mass of a uniform L-shaped lamina of mass 3 kg is
View SolutionFind the position of centre of mass of the uniform lamina shown in figure. If the mass density of the lamina is sigma .
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) origine with dimensions as shown in figure. The mass of lamina is 3 kg.
View SolutionThe coordinates of the centre of mass of a uniform flag -shaped lamina (thin flat plate) of mass 4kg .( The coordinates of the same are shown in the figure) are :
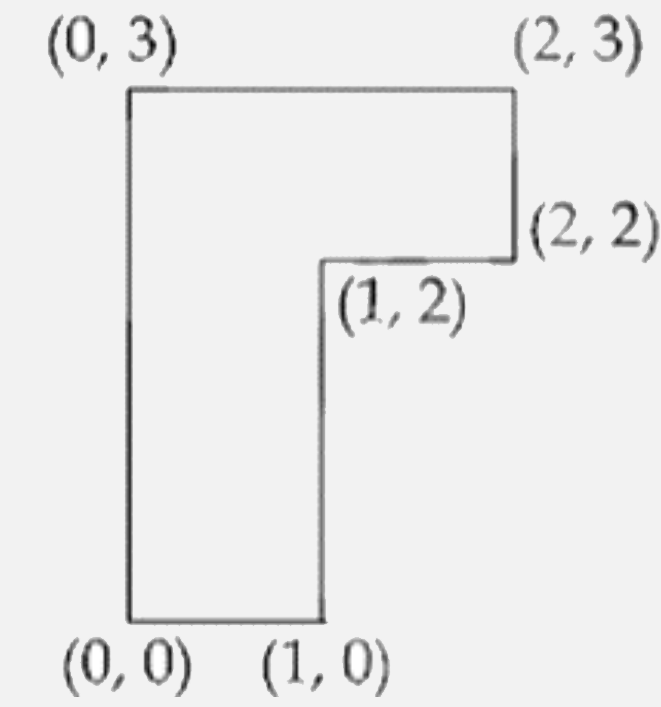
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View Solution
