Determine the current in each brance of the network showin in
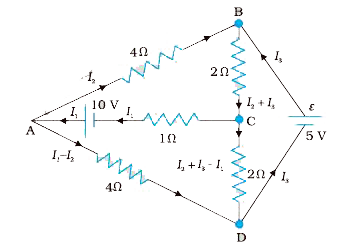
Each branch of the network is assigned an unknow current to be determined by the application of Kirchhoff s rules. To reduce the number of unknowns at the unknow current in each branch. We then have three unknowns I1,I2andI3 which can be fond by alllying the second rule of Kirchhoff to three different closed loops. Kirchhoff.s second rule for the closed lop ADCA gives.
10−4(I1−I2)+2(I2+I3−I1−I1=0
that is, 7I1−6I2−2I3=10
For the closed loop ABCA. we get
10−4I2−2(I2+I3−I1=0
that is 2I1−4I2−4I3=−5
Equations (3.80a,b,c) are three simultaneous equations in three unknowns. These can be solved by the usual method to give
I1=2.5A.I2=58A,I3=178A
The currents in the various branches of the network are
AB:58A,CA:212A,DEB:178A
AD:178A,CD:0A,BC:212A
It is easily verified that Kirchhoff.s second rule applied to the remaining closed lops does not provide any additional independent equation, that is, the above values of currents satisfy the second rule for every closed loop of the network. For example, the total voltage drop over the closed loop BADEB
5V+(58×4)V−(158×4)V
equal to zero, as required by Kirchhoff s second rule.
Similar Questions
Determine the current in each branch of the network shown in Fig.
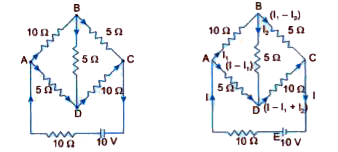
View Solution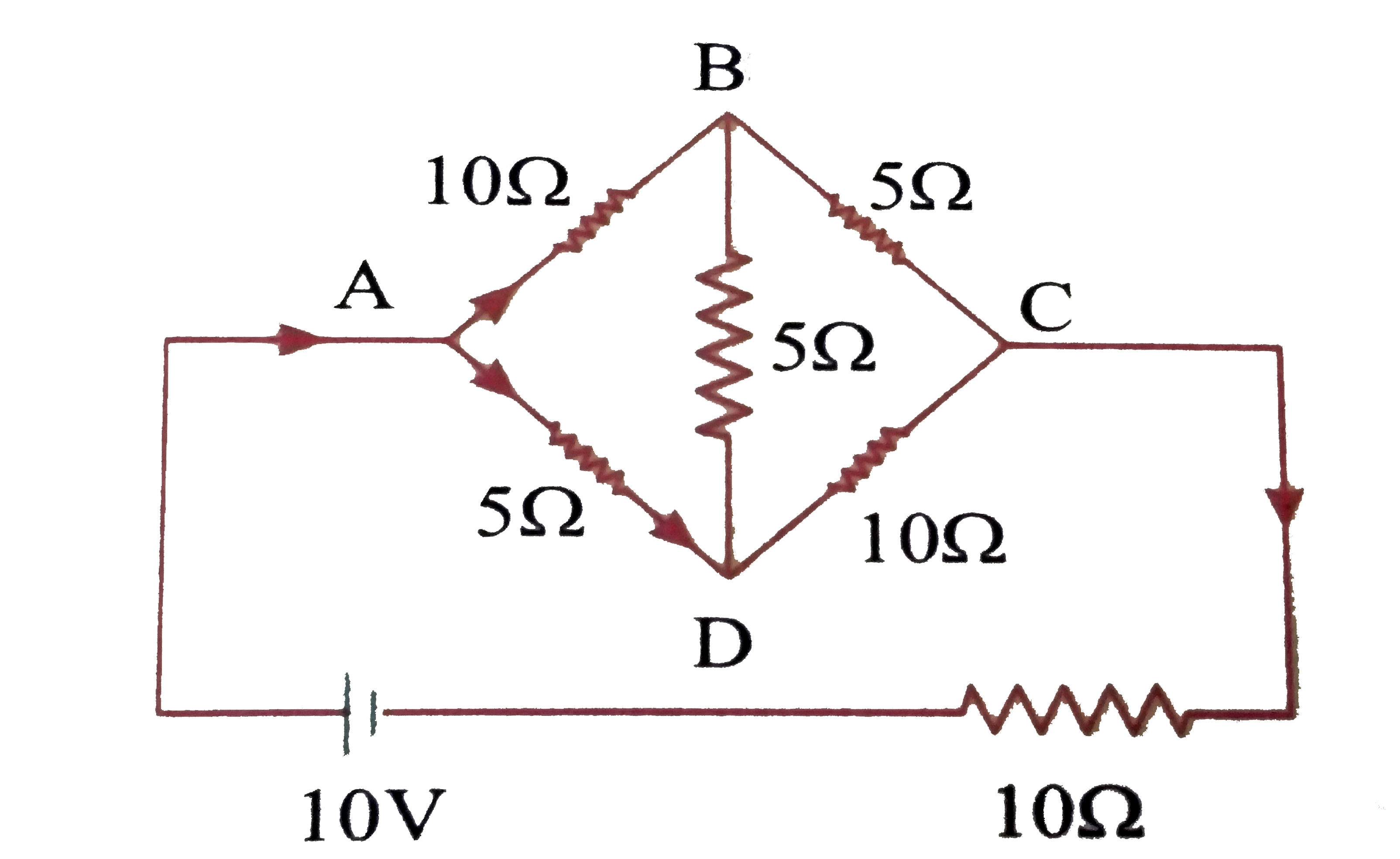
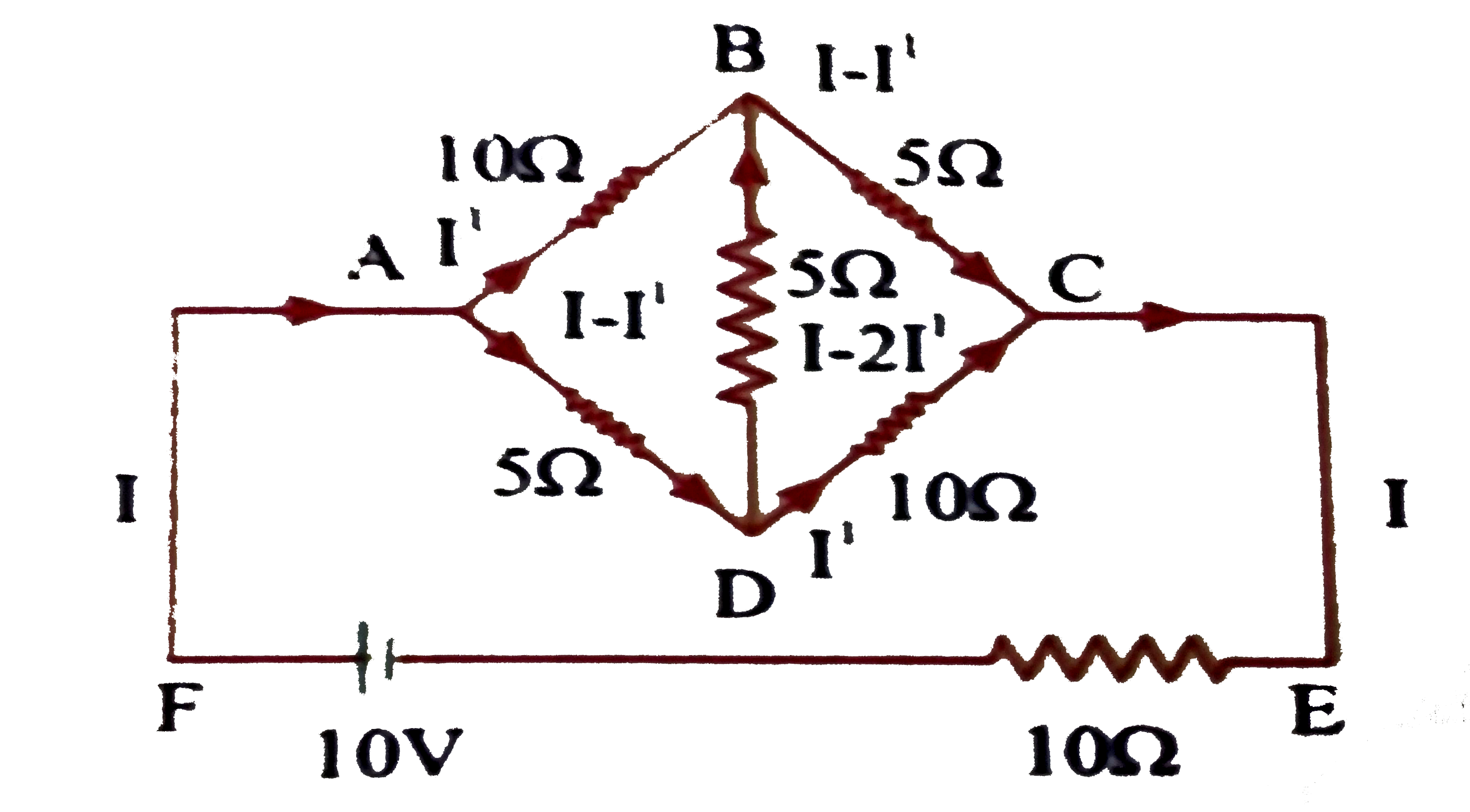
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in figure.
View SolutionDetermine the current in each branch of the network shown in figure.

View Solution

Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig. 3.24

View SolutionDetermine current in each branch of the network shown in figure

View SolutionA network of four 10μF capacitors is connected to a 500V supply as shown in Fig. Determine the (a) equivalent capacitance of the network and (b) charge on each capacitor.
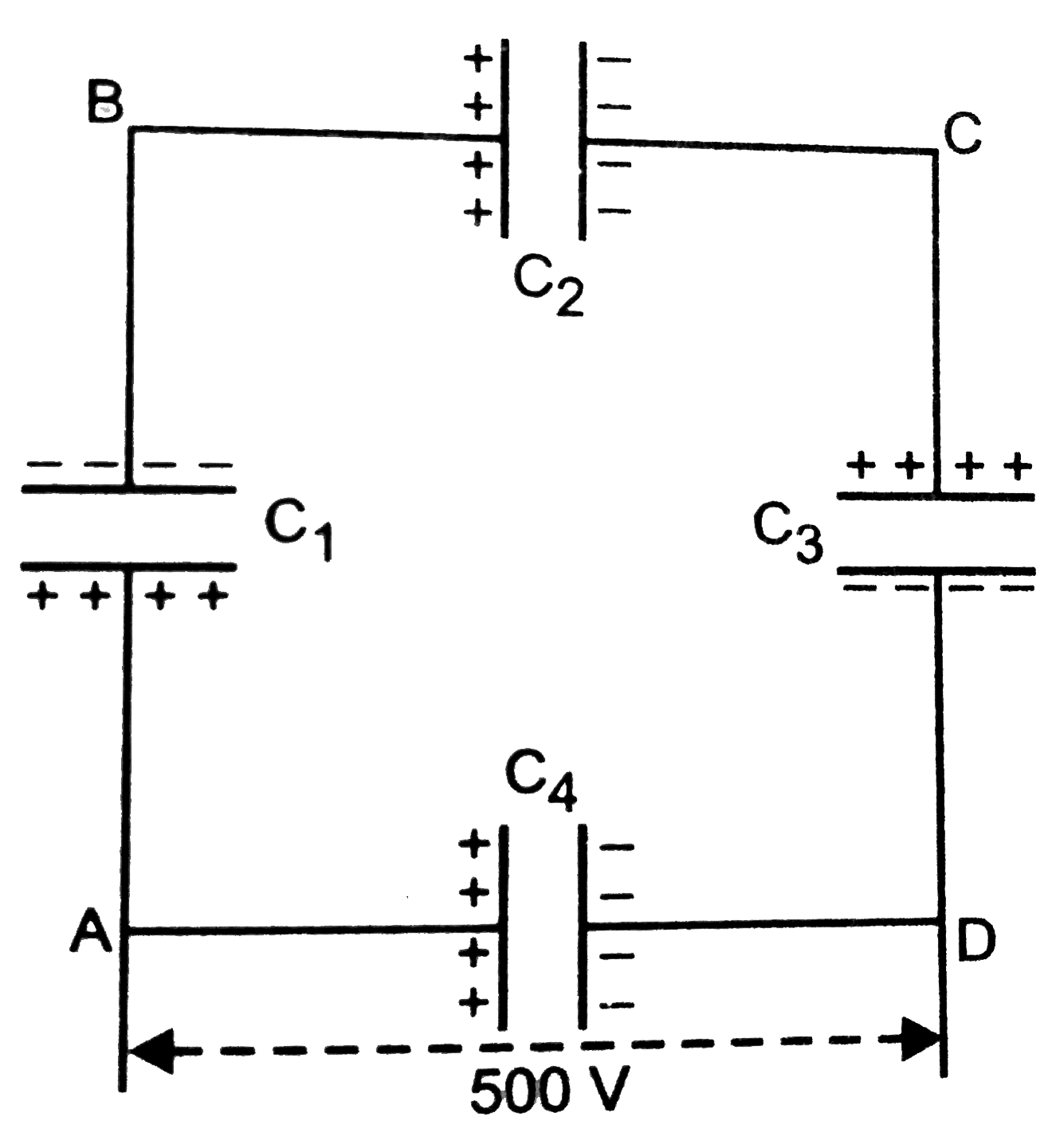
View Solution
calculate the current flowing in each of the resistances of the network shown in figure. The internal resistance of each cell is negligible.
View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
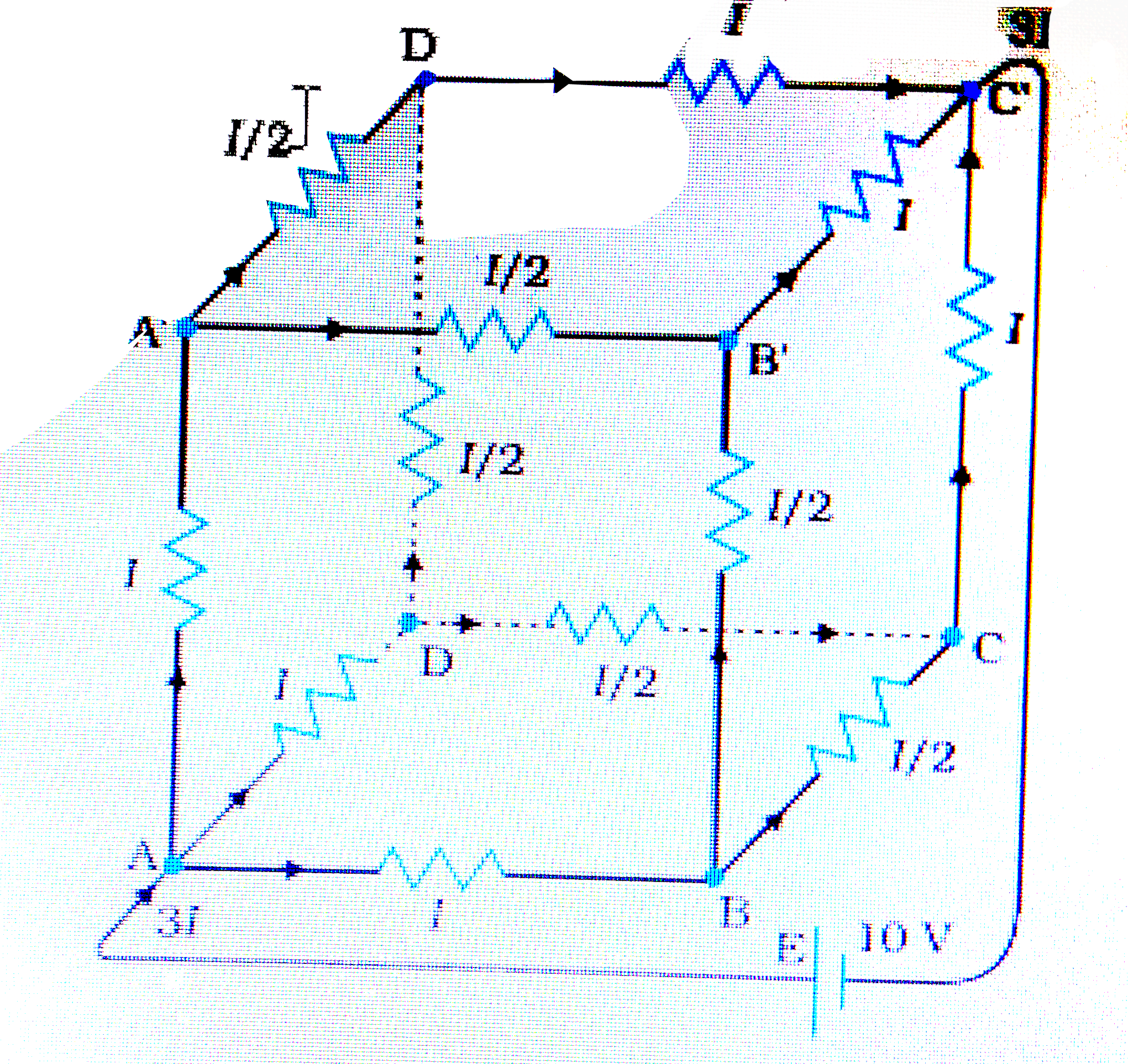
View Solution
