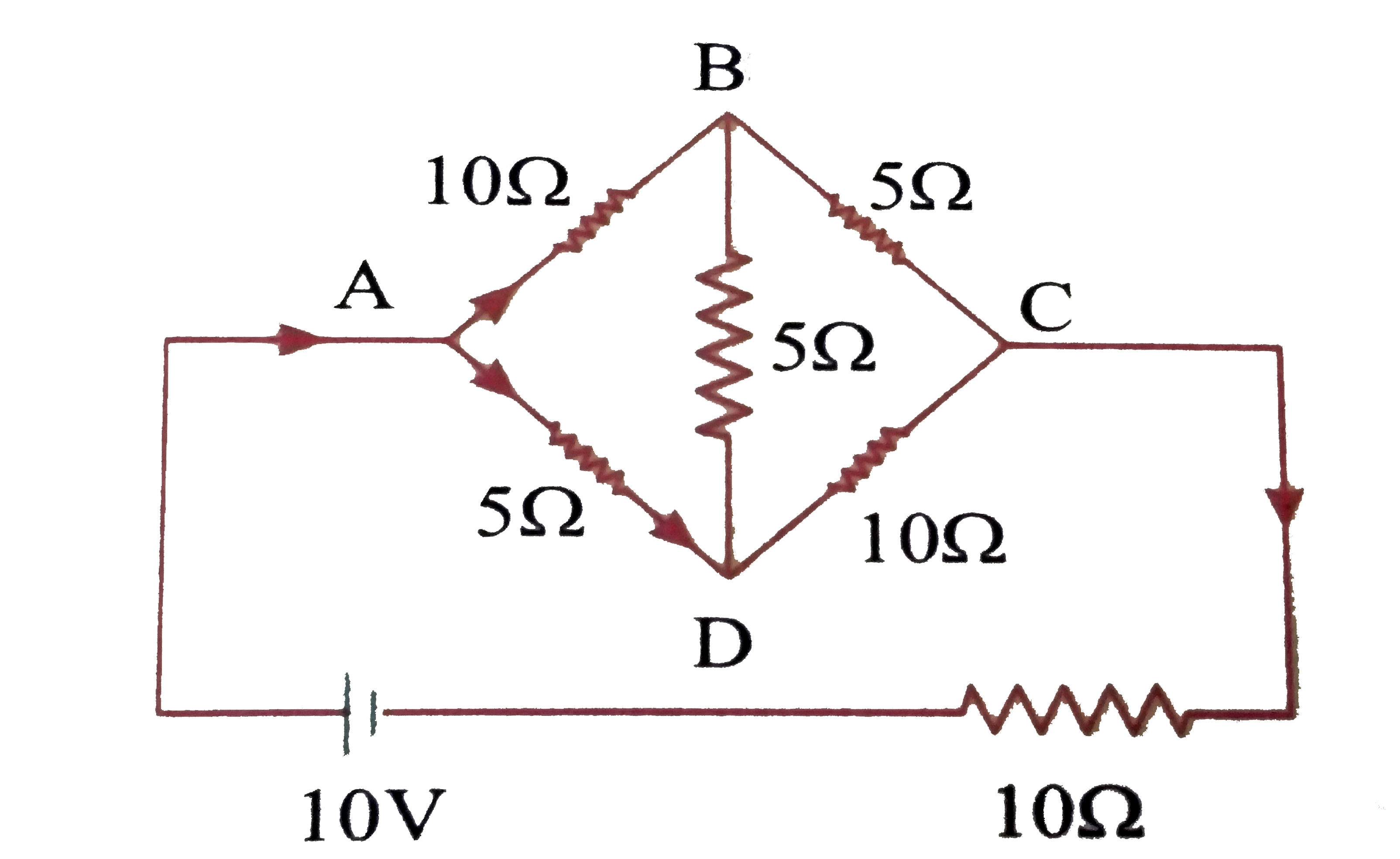
Determine the current in each branch of the network shown in fig.
Video Solution
Text Solution
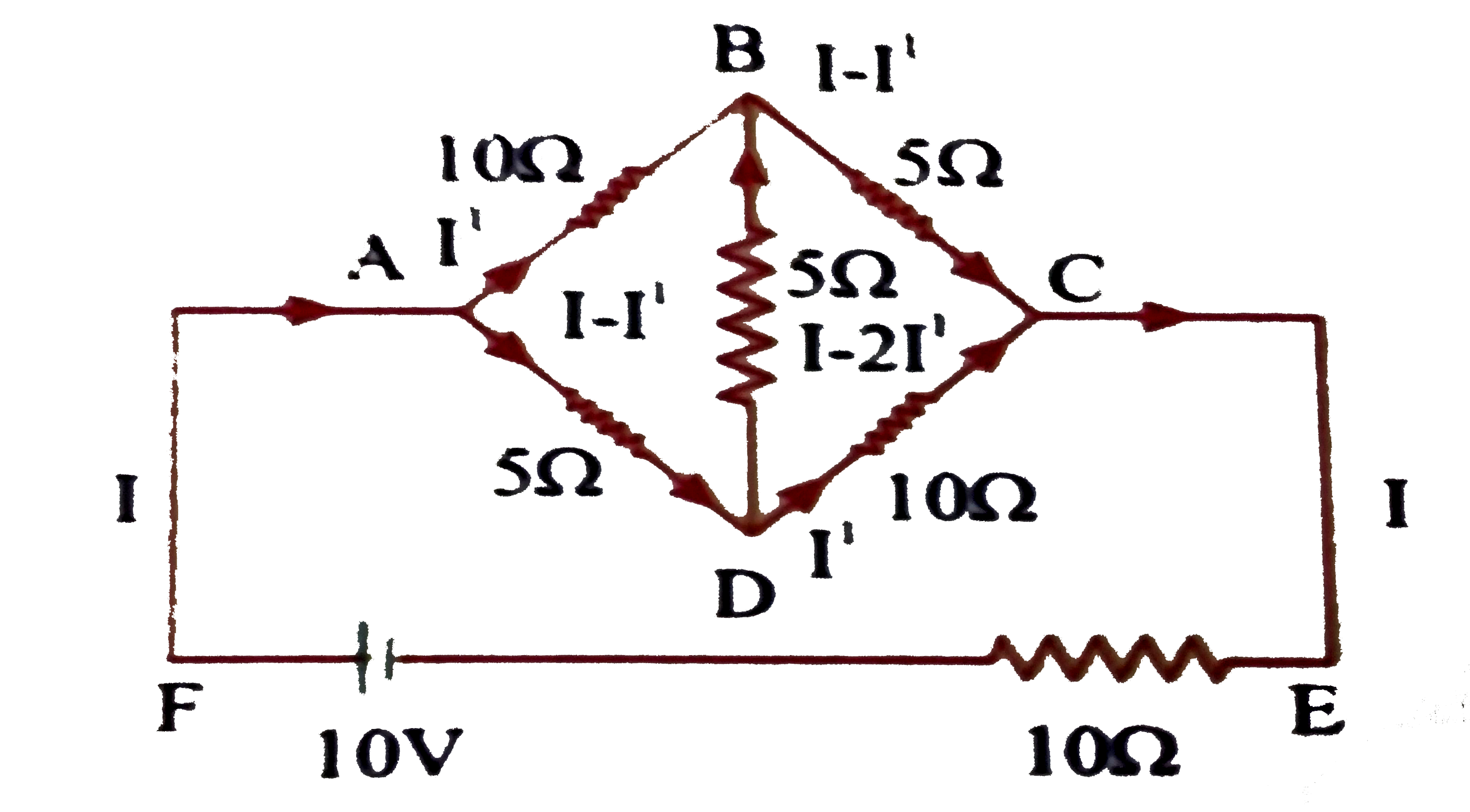
Current flowing through various branches of the circuit is represented in the given figure
I1= Current flowing through the outer circuit
I2= Current flowing through branch AB
I3= Current flowing through branch AD
I2−I4= Current flowing through branch BC
I3+I4= Current flowing through branch CD
I4= Current flowing through branch BD
For the closed circuit ABDA, potential is zero i.e.,
10I2+5I4−5I3=0
2I2+I4−I3=0
I3=2I2+I4....(1)
For the closed circuit ABDA, potential is zero i.e.,
10I2+5I4−5I3=0
2I2+I4−I3=0
I3=2I2+I4....(1)
For the closed circuit BCDB, potential is zero i.e.,
5(I2−I4)−10(I3+I4)−5I4=0
5I2+5I4−10I3−10I4−5I4=0
5I2−10I3−20I4=0
I2=2I3+4I4....(2)
For the closed circuit ABCFEA, potential is zero i.e.,
−10+10(I1)+10(I2)+5(I2−I4)=0
10=15I2+10I1−5I4
3I2+2I1−I4=2....(3)
From equations (1) and (2), we obtain
I3=2(2I3+4I4)+I4
I3=4I3+8I4+I4
−3I3=9I4
−3I4=+I3....(4)
putting equation (4) in equation (1), we obtain
I3=2I2+I4
−4I4=2I2
I2=−2I4...(5)
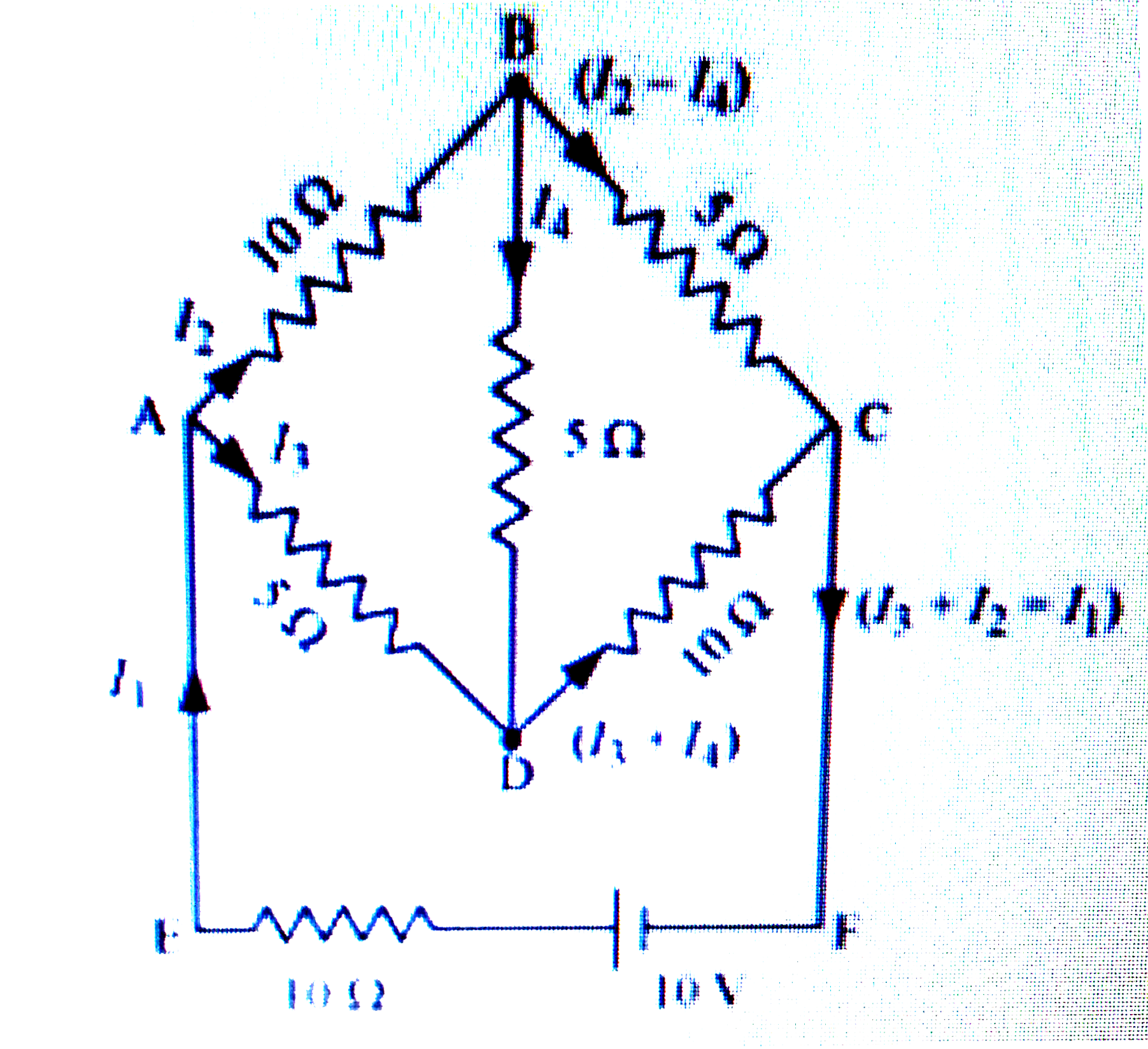
It is evident from the given figure that,
I1=I3+I2....(6)
putting equation (6) in equation (1), we obtain
3I2+2(I3+I2)−I4=2
5I2+2I3−I4=2....(7)
putting equations (4) and (5) in equation (7), we obtain
5(−2I4)+2(−3I4)−I4=2
−10I4−6I4−I4=2
17I4=−2
I4=−217A
Equation (4) reduces to
I3=−3(I4)
=−3(−217)=617A
I2=−2(I4)
=−2(−217)=417A
I2−I4=417−(−217)=617A
I1=I3+I2
=617+417=1017A
Therefore, current in branch AB=417A
In branch BC=1617A
In branch CD=−417A
In branch AD=617A
In branch BD=(−217)A
Total current =417+617+−417+617+−217=1017A.
|
Topper's Solved these Questions
Similar Questions
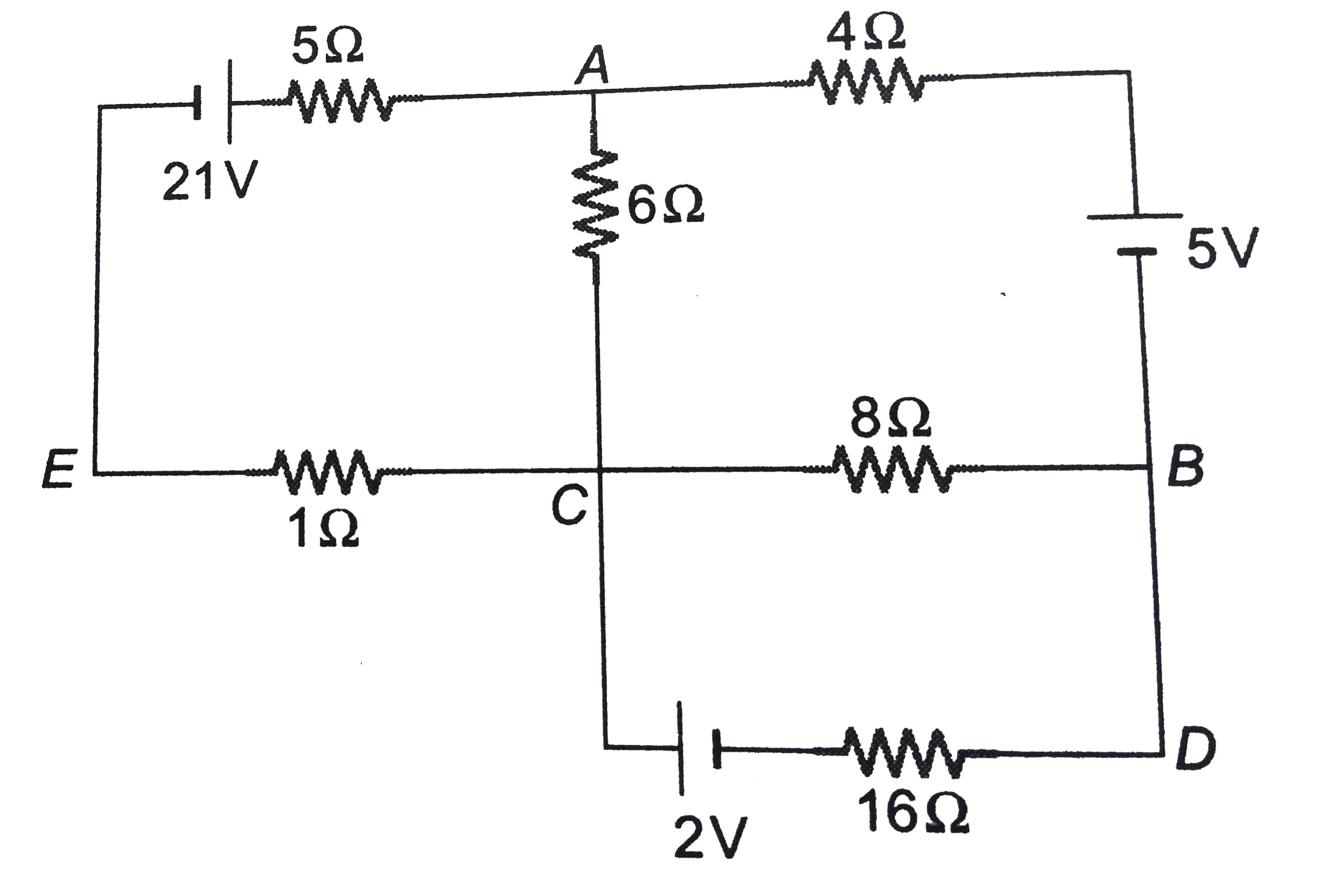
Find the current in each branches of the circuit.
View SolutionFind the current in each resistor in the circuit as shown in fig.

View SolutionCurrent I in the network shown in figure
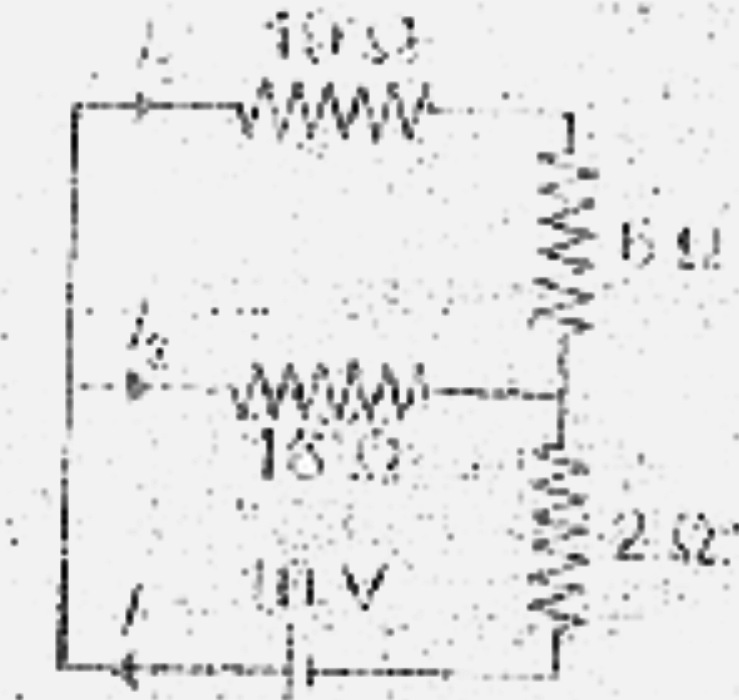
View SolutionCalculate battery current and equivalent resistance of the network shown in figure.
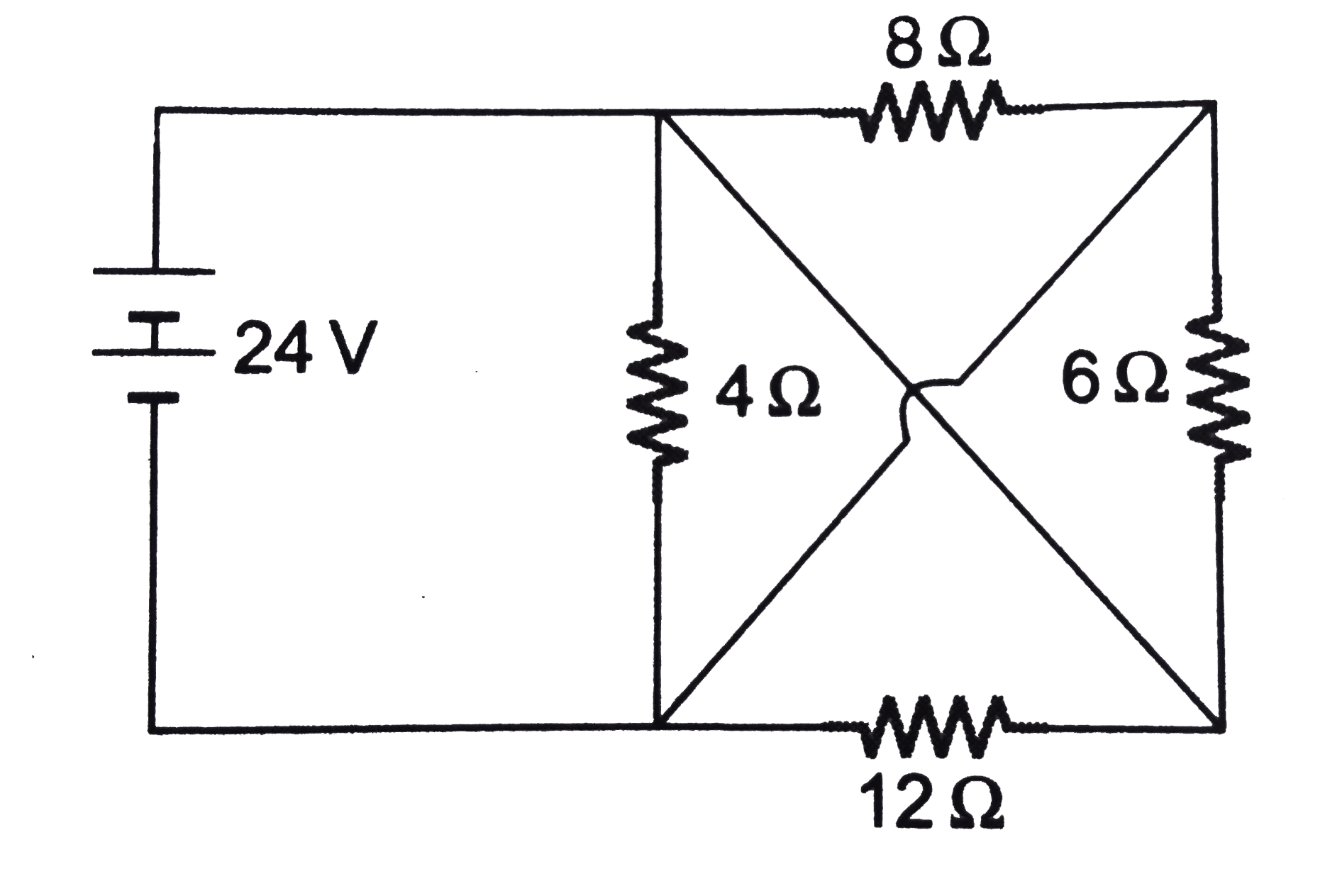
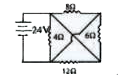
View SolutionCalculate battery current and equivalent resistance of the network shown in figure.
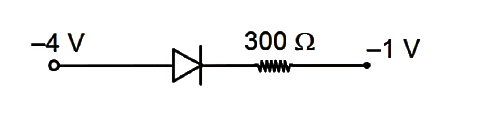
View SolutionThe current in the branch of a circuit shown below is
View SolutionDetermine the currents I1,I2,andI3 for the network shown below
a. I1=……….,b.I2=………….,c.I3=…………….
View SolutionCurrent l in the network shown in figure is

View Solution(a)Find the current I supplied by the battery in the network shown in figure in steady state. (b)find the charge on the capacitor.

View SolutionCurrent l in the network shown is figure is
View Solution
