Draw the graph of the signum function f(x)={|x|x when x≠00 when x=0
Video Solution
Text Solution
Clearly, (0,0), is a point on the graph. Now, when |x|= -x and therefore,
f(x) = -1 for all value of x lt 0.
Hence, the graph may be drawn, as shown in the adjoining figure.
Clearly, the funcation is broken (i.e, it is discontinuous ) at each of the points x=-1 and 1.
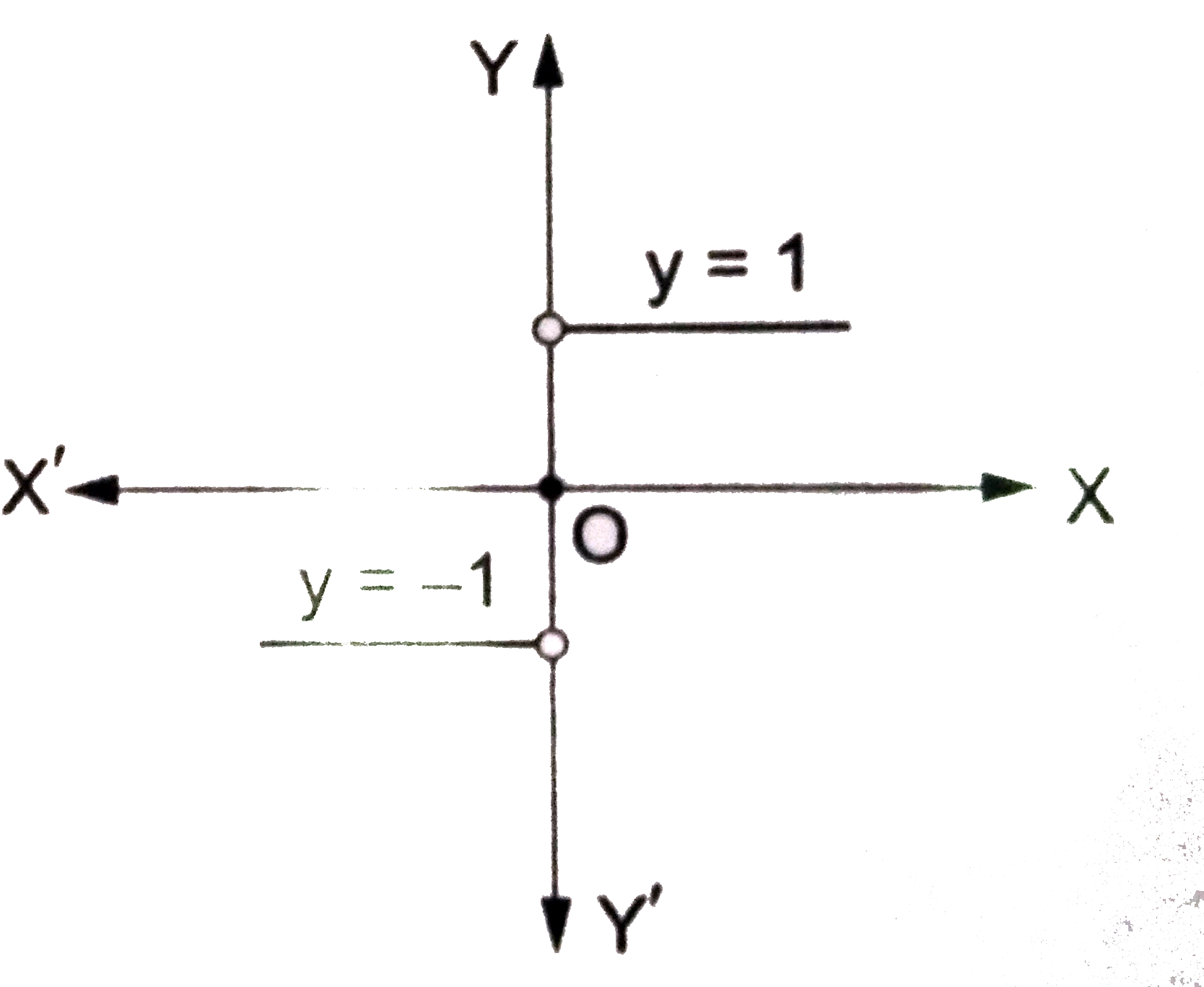
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise 9A27videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - RS AGGARWALCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise 9B11videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - RS AGGARWALCHAPTER - BINARY OPERATIONSEXERCISE - Exercise 3B8videos
BINARY OPERATIONS
- BOOK - RS AGGARWALCHAPTER - CROSS,OR VECTOR, PRODUCT OF VECTORSEXERCISE - Exercise 2426videos
CROSS,OR VECTOR, PRODUCT OF VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the range of the function f(x)=|x|x,x≠0?
ASet of all real numbersBSet of all integersC{−1,1}D{−1,0,1}
f(x)={sin2x5x,when x≠0m, when x=0 at x = 0
View SolutionDraw the graph of the signum function, f:R→R, defined by
f(x)=⎧⎪⎨⎪⎩x|x|,when x≠00,when x=0orf(x)=⎧⎪⎨⎪⎩1,if x>00,if x=0−1,if x<0View SolutionExamine the continuity of the function f(x) at x = 0.
f(x)={sinxx when x≠02 when x=0View SolutionDraw the graph of the function: f(x)=⎧⎪⎨⎪⎩x if x≤0x2 if 0<x≤2x if x>2
View SolutionShow that the function f(x)={7x+5,x≥0,5−3x, x<0 is a continuous function.
View SolutionDiscuss the continuiy of the function
f(x)={1x, x≠01, x=0 at x=0.View SolutionDraw the graph of the modulus function, defined by
f:R→R:f(x)=|x|={x,when x≥0−x,when x<0View Solution

