The function $f (x) = x^{3} - 27 x + 8$ is increasing when

A

$| x | < 3$

B

$| x | > 3$

C

$- 3 < x < 3$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$f' (x) = 3 x^{2} - 27 = 3 (x^{2} - 9) = 3 (x + 3) (x - 3)$
$∴ f' (x) = 0 \Rightarrow x = - 3 or x = 3$
There are two factors in $f' (x)$ , so we start with +ve sign.
$∴ f (x)$ is increasing when $x < - 3 or x > 3, i.e., when | x | > 3$

|

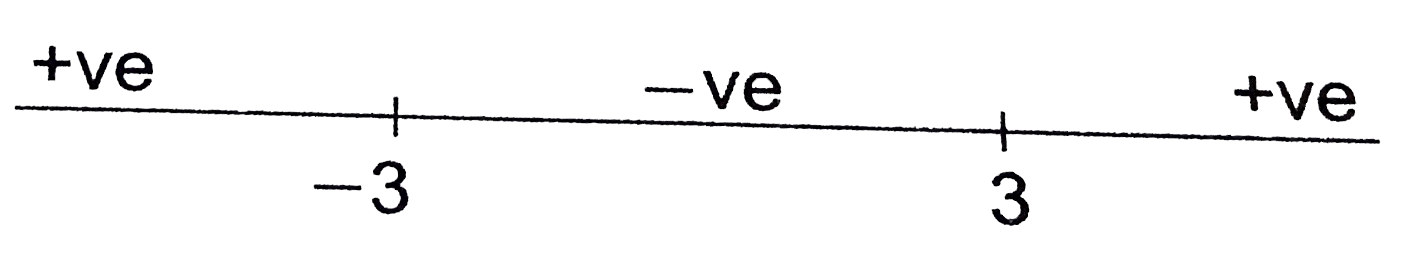
Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The function $f (x) = x^{3} - 3 x^{2} + 6$ is an increasing function for
A $0 < x < 2$
B $x < 2$
C $x > 2$ or $x < 0$
Dall x
Question 2 - Select One
The function, $f (x) = (3 x - 7) x^{2 / 3}$ , x in is increasing for all x lying in :
A $(- \infty, - \frac{14}{15}) \cup (0, \infty)$
B $(- \infty, \frac{14}{15})$
C $(- \infty, 0) \cup (\frac{14}{15}, \infty)$
D $(- \infty, 0) \cup (\frac{3}{7}, \infty)$
Question 3 - Select One
The function f(x) = $x^{2}$ is increasing in the interval
A(-1,1)
B $(- \infty, \infty)$
C $(0, \infty)$
D $(- \infty, 0)$

RS AGGARWAL-APPLICATIONS OF DERIVATIVES-Objective Questions

Home
Ask Doubt
Profile