An urn contians 4 white and 3 red balls. Let X be the number of red balls in a random draw of 3 balls. Find the mean and variance of X.
When 3 balls are drawn at random, there may be no red ball, 1 red ball, 2 red balls or 3 red balls. Let X denote the random variable showing the number of red balls in a draw of 3 balls.
Then, x can take the value 0, 1, 2 or 3.
P(X=0)=P(getting no red ball)
=P(getting 3 white balls)
=4C37C3=(4×3×23×2×1×3×2×17×6×5)=45.
P(X=1)=P(getting 1 red and 2 white balls)
=3C1×4C27C3=(3×4×32×3×2×17×6×5)=1835.
P(X=2)=P(getting 2 red and 1 white ball)
=3C2×4C17C3=(3×22×1×4×3×2×17×6×5)=1235.
P(X=3)=P(getting 3 red balls)=3C37C3=1×3×2×17×6×5)=135.
Thus, the probability distribution of X is given below.
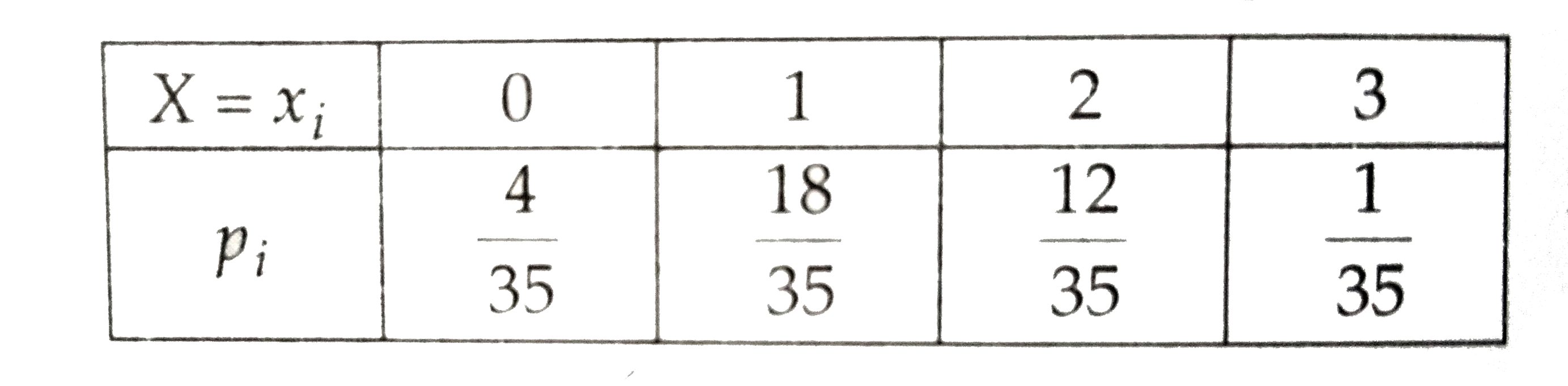
∴ mean,μ=Σxipi=(0×435)+(1×1835)+(2×1235)+(3×135)=97.
Variance, σ2=Σx2ipi−μ2
=[(0×435)+(1×1835)+(4×1235)+(9×135)−8149]
=(157−8149)=2449.
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 31
18 Videos
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Objective Questions
30 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B
2 Videos
- PRODUCT OF THREE VECTORSBOOK - RS AGGARWALCHAPTER - PRODUCT OF THREE VECTORSEXERCISE - Objective Questions
34 Videos
Similar Questions
An urn contains 4 white and 3 red balls. Let X be the number of red balls in a random draw of three balls. Find the mean and variance of X.
View SolutionThree balls are drawn simultaneously from a bag containing 5 white and 4 red balls. Let X be the number of red balls drawn. Find the mean and variance of X.
View Solution
Knowledge Check
An urn contains 4 white and 3 red balls. Let X be the number of red balls in a random draw of 3 balls . Find the mean and variance of X.
A57,2549B97,2449C127,2449DNone of theseAn urn contains 4 white and 3 red balls. Three balls are drawn with replacement from this urn. Then, the standard deviation of the number of red balls/drawn is
A67B3649C57D2549
A run contains 4 white and 3 red balls. Find the probability distribution of the number of red balls in a random draw of three balls.
View SolutionOne bag contains 5 white and 3 red balls, and a second bag contains 4 white and 5 red balls. From one of them chosen at random two balls are drawn, find the chance that they are of different colours.
View SolutionAn urn contains 4 white and 6 red balls. Four balls are drawn at random from the urn. Find the probability distribution of the number of white balls.
View SolutionAn urn contains 4 white and 6 red balls. Four balls are drawn at random from the urn. Find the probability distribution of the number of white balls.
View SolutionAn urn contains 4 white and 3 red balls. Three balls are drawn at random from the urn with replacement. Find the probability distribution of the number of red balls.
View SolutionA bag A contains 2 white and 3 red balls and a bag B contains 4 white and 5red balls. One ball is drawn at random from one of the bags and is found to be red. Find the probability that it was drawn as red.
View Solution
