One side of an equilateral triangle is 18 cm. The mid-point of its sides are joined to form another triangle whose mid-points, in turn, are joined to form still another triangle. The process is continued indefinitely. Find the sum of the (i) perimeters of all the triangles. (ii) areas of all triangles.
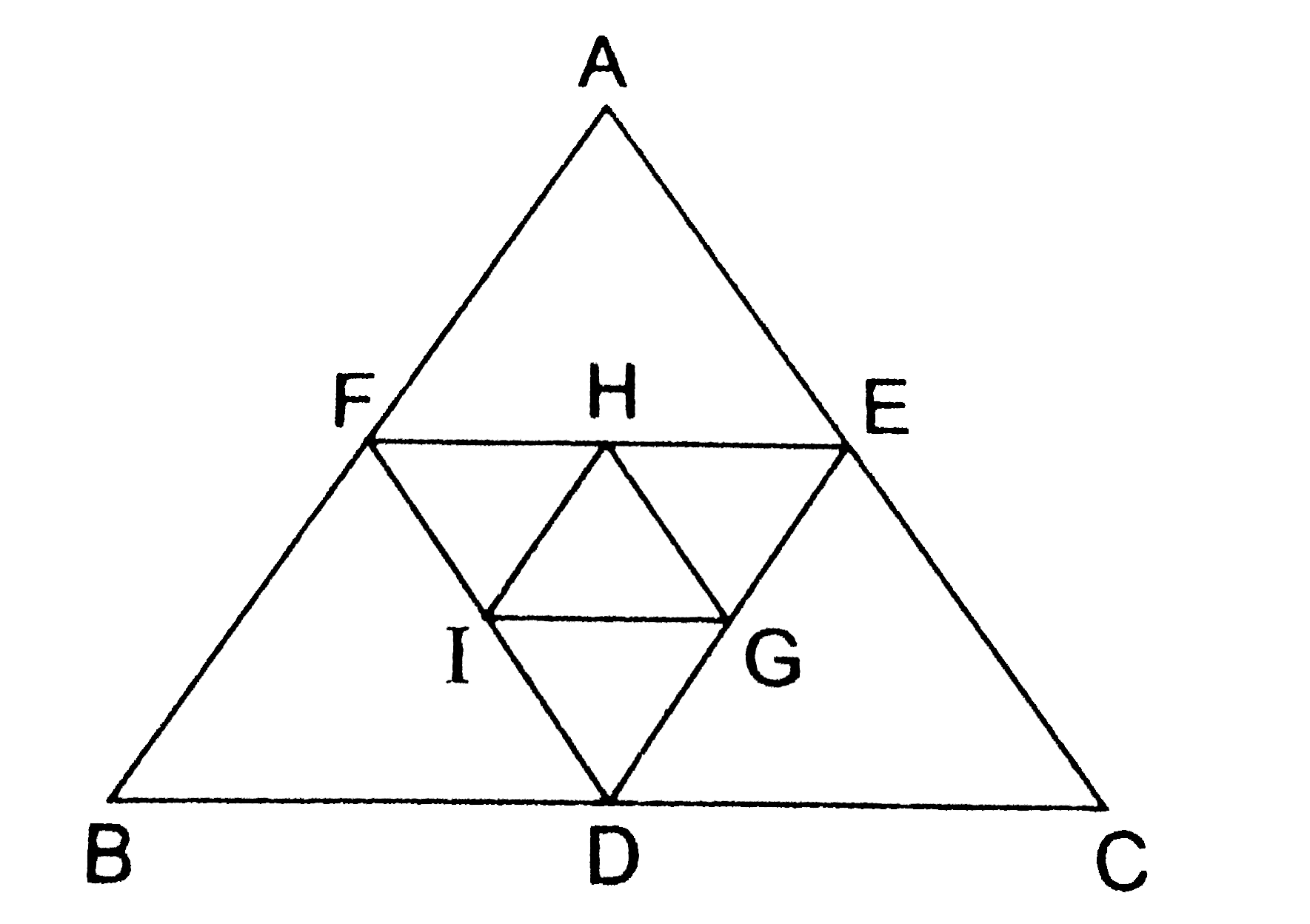
Let ΔABC be the given triangle having each side 18 cm. Let D, E, F be the midpoints of BC, CA, AB respectively to form ΔDEF. Let G, H, I be the midpoints of DE, EF and FD respectively to form ΔGHI.
We continue this process indefinitely.
The sides of these triangle are 18 cm, 9 cm, 92 cm, ..., and so on.
(i) Sum of the perimeters of all triangles so formed
=3{18+9+92+94+...∞}cm
={3×a(1−r)}cm, where a=18 and r=918=12
=⎧⎪
⎪⎨⎪
⎪⎩3×18(1−12)⎫⎪
⎪⎬⎪
⎪⎭cm=(3×36)cm=108cm.
(ii) Sum of the areas of all the triangles so formed
=√34.{(18)2+(9)2+(92)2+(94)2+...∞}cm2
=√34.{324+81+814+8116+...∞}cm2
=√34.a(1−r)cm2, where a=324 and r=81324=14
=⎧⎪
⎪⎨⎪
⎪⎩√34×324(1−14)⎫⎪
⎪⎬⎪
⎪⎭cm2=108√3cm2.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12A18videos
GEOMETRICAL PROGRESSION
- BOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12B9videos
GEOMETRICAL PROGRESSION
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3F VERY-SHORT-ANSWER QUESTIONS21videos
FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 196videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
One side of an equliateral triangle is 32 cm . The mid -points of its sides are joined to form
another trianbgle whose mid -point are in turn joinded to form still another triangle . This process
continus indefinitely . Then find the sum of the perimeters and areas of all the triangles .View SolutionOne side of an equilateral triangle is 24 cm. The midpoints of its sides are joined to form another triangle whose midpoints are in turn joined to form still another triangle this process continues indefinitely. The sum of the perimeters of all the triangles is
View Solution
Knowledge Check
- Question 1 - Select One
One side of an equilateral triangle is 24 cm. The midpoints of its sides are joined to form another triangle whose midpoints are in turn joined to form still another triangle this process continues indefinitely. The sum of the perimeters of all the triangles is
A144 cmB72 cmC536 cmD676 cm - Question 2 - Select One
Find the area of an equilateral triangle whose side is a cm.
A√34a2 cm2B√24a2 cm2C√35a2 cm2D√25a2 cm2 - Question 3 - Select One
An equilateral triangle is drawn by joining the midpoints of the sides of another equilateral triangle. A third equilateral triangle is drawn inside the second one joining the midpoints of the sides of the second equilateral tringle, and the process continues infinitely. Find the sum of the perimeters of all the equilateral triangles, if the side of the largest equilateral triangle is 24 units.
A288 unitsB72 unitsC36 unitsD144 units
One side of an equilateral triangle is 36 cm. The mid-points of its sides are joined to form another triangle. Again another triangle is formed by joining the mid-points of the sides of this triangle and the process is continued indefinitely. Determine the sum of areas of all such triangles including the given triangle.
View SolutionThe side of a given square is 10 cm. The midpoints of its sides are joined to form a new square. Again, the midpoints of the sides of this new aquare are joined to form another square. The process is continued indefinitely. Find (i) the sum of the areas and (ii) the sum of the perimeters of the squares.
View SolutionEach side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle .
View SolutionFind the perimeter of an equilateral triangle with side 8 cm.
View SolutionFind the perimeter of an equilateral triangle with side 9cm.
View Solution

