Question

Reduce the equation $3x-2y+4=0$ to intercepts form and find the length of the segment intercept the axes.

Explanation

We have
`3x-2y+4=0 Rightarrow 3x-2y=-4`
`Rightarrow (3x)/(-4)+(y)/(2)=1["on dividing both sides by"-4]`
`Rightarrow (x)/(((-4)/(3)))+(y)/(2)=1`
`Rightarrow (x)/(a)+(y)/(b)=1,"where"a=(-4)/(3)and b=1`

`therefore (x)/(((-4)/(3)))+(y)/(2)=1` is the required equation in intercepts form.
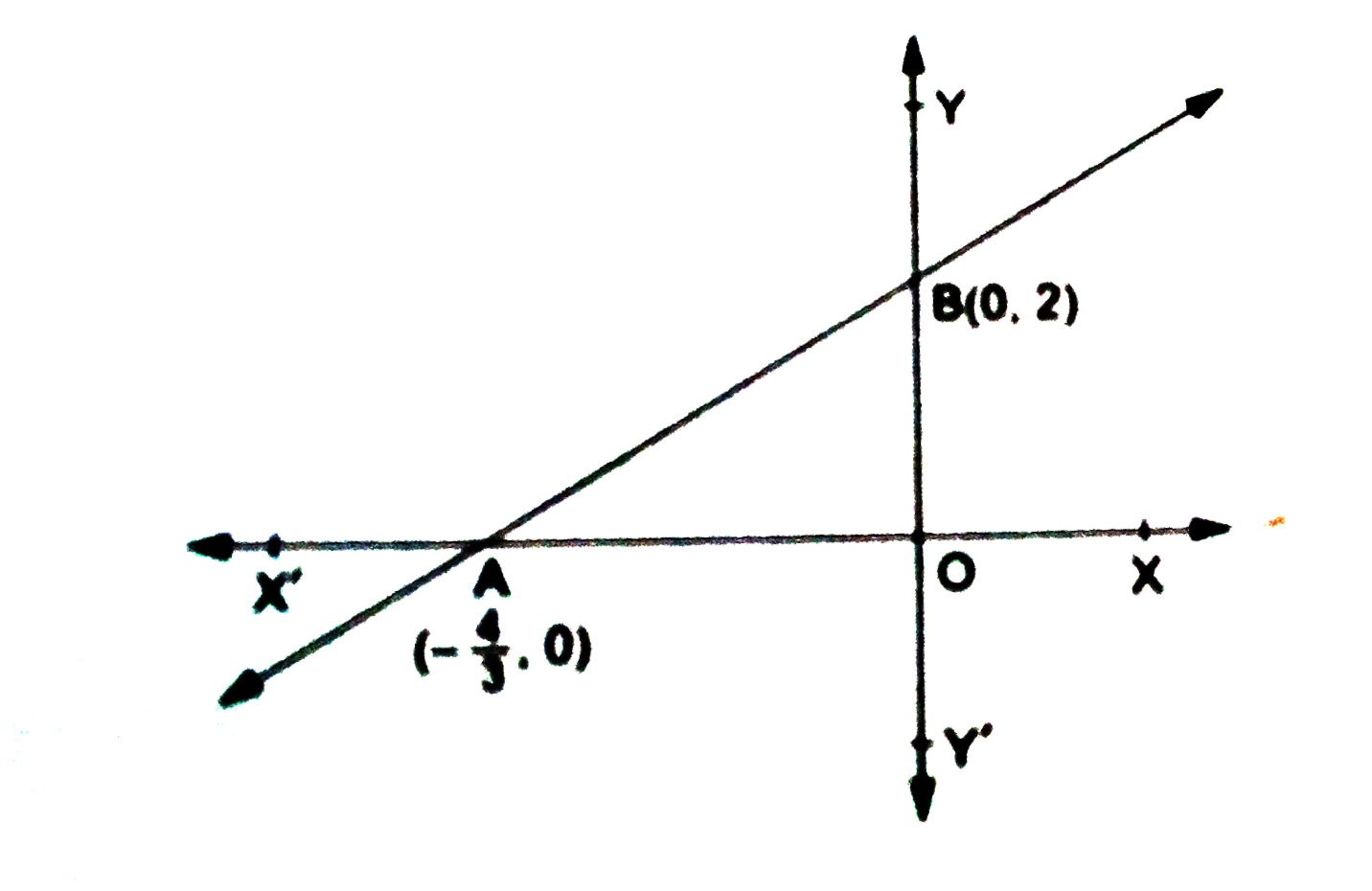
x-intercept `=(-4)/(3)` and y-intercept =2
If AB is the part of the line intercepted between the axes them the end points of this line segment are `A((-4)/(3),0) and B(0,2)`
Length of AB=`sqrt(((-4)/(3),-0)^(2)+(0-2)^(2))=sqrt((16)/(9)+4)=(2)/(3)"sqrt"13"units"`