Find the equatiion of a circle with centre $(h, k)$ and touching the y-axis.

Video Solution

Text Solution

Verified by Experts

Clearly, the radius of the circle = h
So, the required equation is
${(x - h)}^{2} + {(y - k)}^{2} = h^{2}$
$\Rightarrow x^{2} + y^{2} - 2 h x - 2 k y + k^{2} = 0$

|

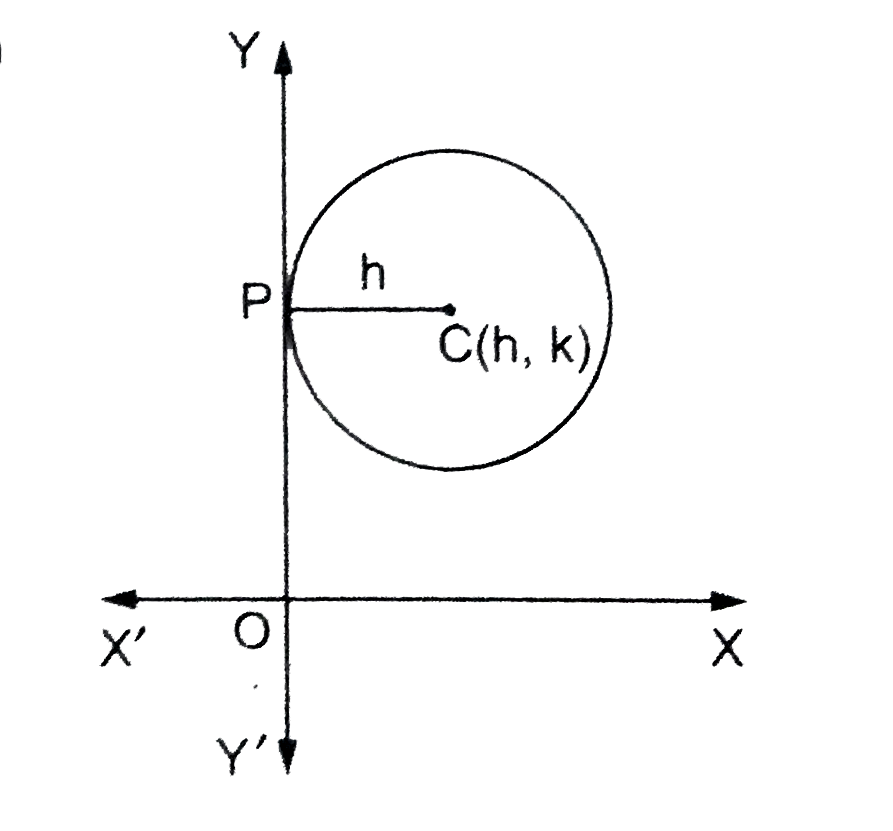
Updated on:21/07/2023

Class 11 MATHS CIRCLES

Topper's Solved these Questions

BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 A
14videos
CIRCLE
BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B
18videos
CIRCLE
BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B
16videos
BINOMIAL THEOREM
BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D
18videos
COMBINATIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The equation to a circle with centre(2,1) and touching x axis is
A $x^{2} + y^{2} + 4 x + 2 y + 4 = 0$
B $x^{2} + y^{2} - 4 x - 2 y + 4 = 0$
C $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$
Dnone of these
Question 2 - Select One
The equation of family of circles with centre at (h,k) touching the X-axis is given by
A $x^{2} + y^{2} - 2 h x + h^{2} = 0$
B $x^{2} + y^{2} - 2 h x - 2 k y + h^{2} = 0$
C $x^{2} + y^{2} - 2 h x - 2 k y - h^{2} = 0$
D $x^{2} + y^{2} - 2 h x - 2 k y = 0$

RS AGGARWAL-CIRCLE -EXERCISE 21 B

Home
Ask Doubt
Profile