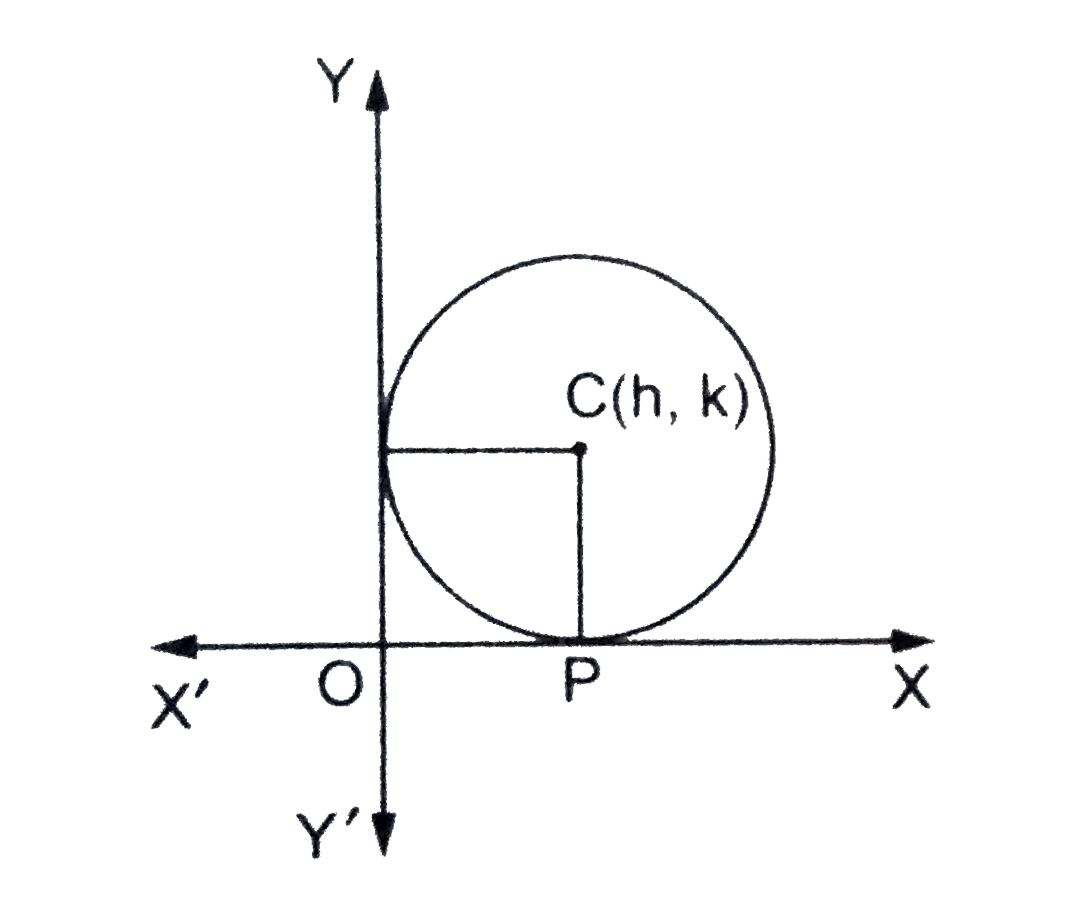
Find the equation of a circle with centre $(h, k)$ and touching both the axes

Video Solution

Text Solution

Verified by Experts

Clearly, radius = $h = k = c$ (say)
$∴$ the equation of the circle is
${(x - c)}^{2} + {(y - c)}^{2} = c^{2}$
$\Rightarrow x^{2} + y^{2} - 2 c (x + y) + c^{2} = 0$ ,
where $c = h = k$ .

|

Updated on:21/07/2023

Class 11 MATHS CIRCLES

Topper's Solved these Questions

BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 A
14videos
CIRCLE
BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B
18videos
CIRCLE
BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B
16videos
BINOMIAL THEOREM
BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D
18videos
COMBINATIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The equation to a circle with centre(2,1) and touching x axis is
A $x^{2} + y^{2} + 4 x + 2 y + 4 = 0$
B $x^{2} + y^{2} - 4 x - 2 y + 4 = 0$
C $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$
Dnone of these
Question 2 - Select One or More
The equation of circle passing through (-1,-2) and touching both the axes is
A $x^{2} + y^{2} - 2 x - 2 y - 1 = 0$
B $x^{2} + y^{2} + 2 x + 2 y + 1 = 0$
C $x^{2} + y^{2} + 10 x + 10 y + 25 = 0$
D $x^{2} + y^{2} - 2 x - 2 y + 1 = 0$

RS AGGARWAL-CIRCLE -EXERCISE 21 B

Home
Ask Doubt
Profile