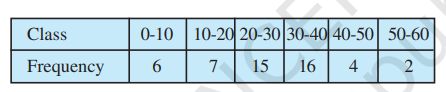
Calculate the mean deviation about the median for the following data :

Video Solution

Text Solution

Verified by Experts

Converting the given series into an exclusive series, we prepare the table, given below :

Thus N=100 and therefore, $\frac{N}{2} = 50$
$\Rightarrow m e d i a n s 35.5 - 40.5$
$\Rightarrow L = 35.5, f = 26, h = 5 and c = 37 .$
$∴ median = L + \frac{(\frac{N}{2} - c)}{f} \times h$
$= {35.5 + \frac{(50 - 37)}{26} \times 5} = (35.5 + 2.5) = 38 .$
Thus, M=38.
Now, we prepare the table given below :

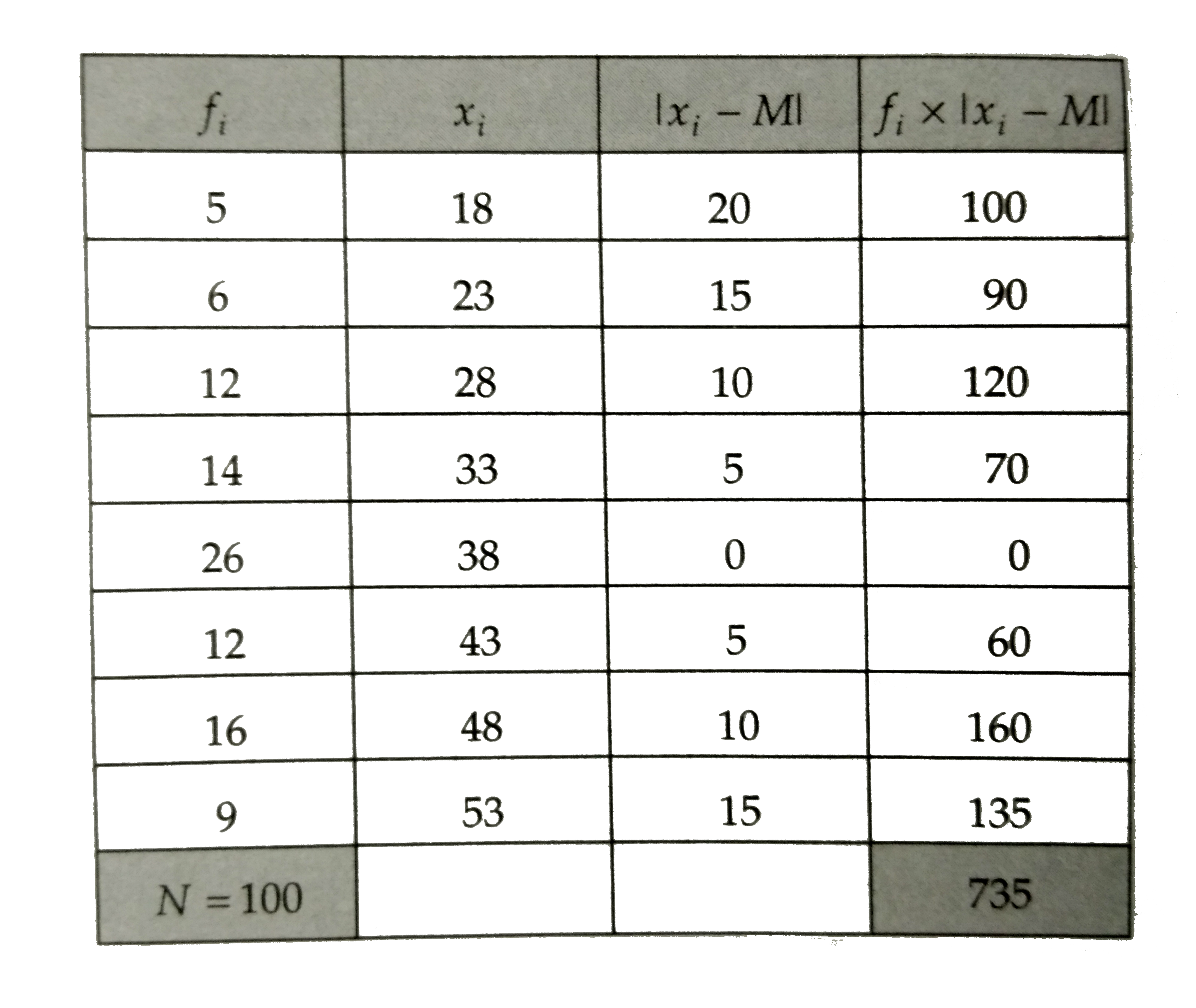
Thus, $Σ f_{i} \times | x_{i} - M | = 735 and N = 100 .$
$∴ M D (M) = \frac{Σ f_{i} \times | x_{i} - M |}{N} = \frac{735}{100} = 7.35 .$
Hence, the mean deviation about the median is 7.35.

|

Updated on:21/07/2023

Class 11 MATHS STATISTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the mean deviation about median for the following data.
A10.34
B $10.50$
C $10.40$
D $10.37$

RS AGGARWAL-STATISTICS-EXERCISE 30D

Home
Ask Doubt
Profile