If cosecθ=2, show that (cotθ+sinθ1+cosθ)=2.
Video Solution
Text Solution
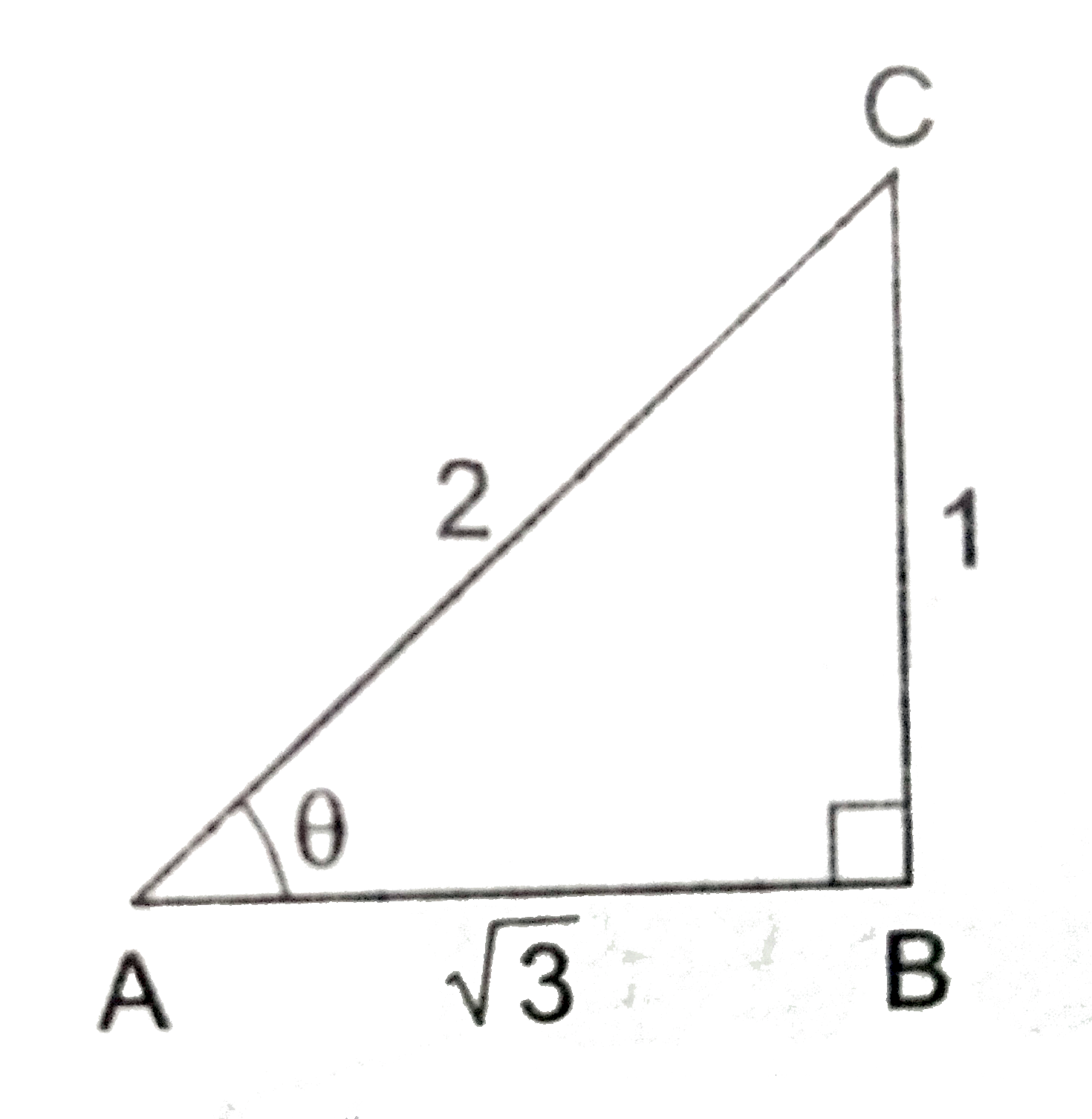
cosecθ=2⇒sinθ=12=BCAC.
AB2=AC2−BC2=(2)2−(1)2=4−1=3⇒AB=√3.
Given expression =⎧⎪
⎪⎨⎪
⎪⎩√3+1(2+√3)×(2−√3)(2−√3)⎫⎪
⎪⎬⎪
⎪⎭=2.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 1035videos
TRIGONOMETRIC RATIOS
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 1215videos
TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
sinθ+sin2θ1+cosθ+cos2θ=?
AtanθBsinθCcosθDtan2θ - Question 2 - Select One
sinθ+sin2θ1+cosθ+cos2θ=
A12tanθB12cotθCtanθDcotθ - Question 3 - Select One
The value of secθ(1+sinθcosθ+cosθ1+sinθ)−2tan2θ is
A4B1C2D0

