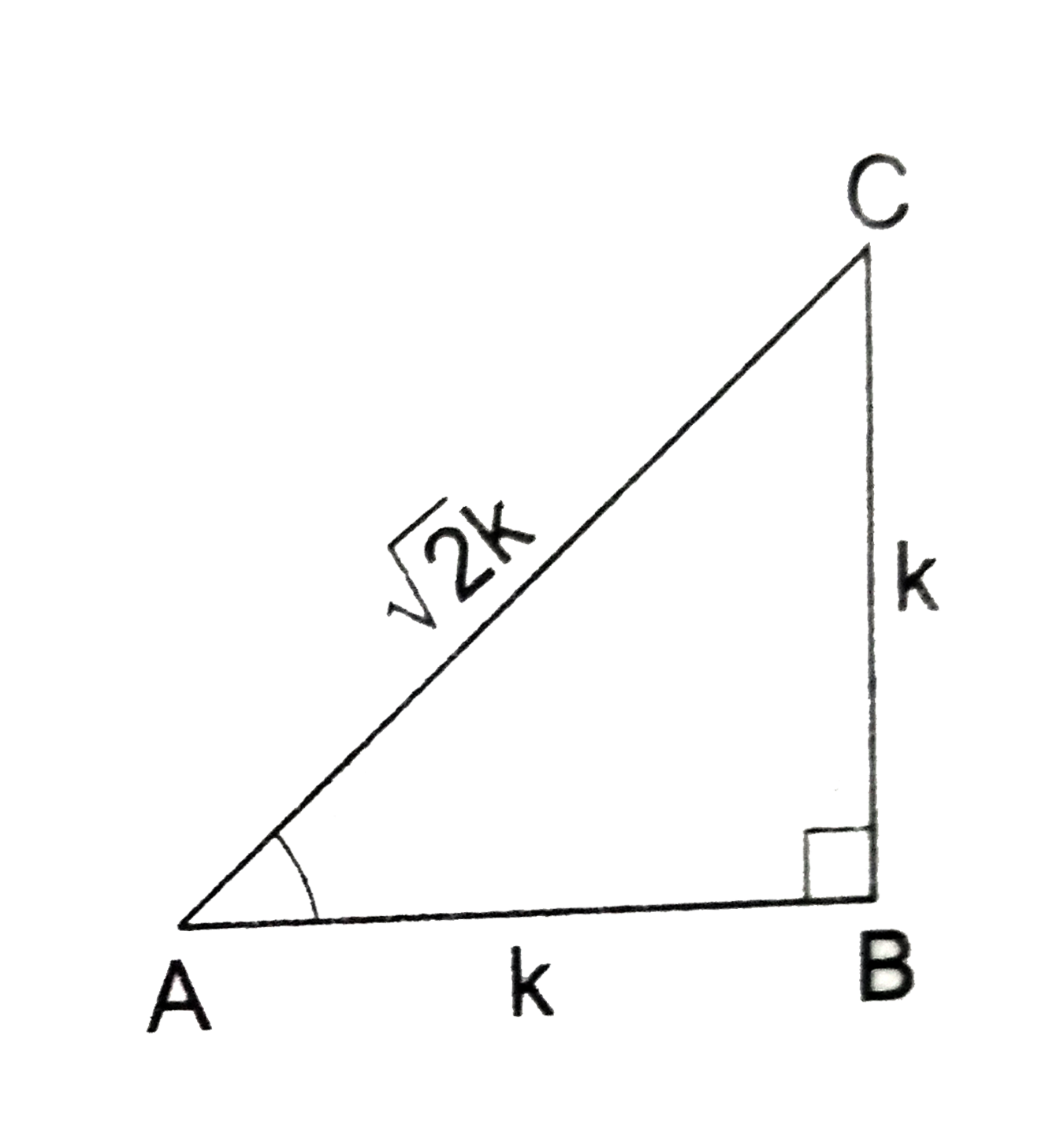
In a right triangle ABC right-angled at B. if $t a n A = 1$ , then verify that $2 s \in A cos A = 1 .$

Video Solution

Text Solution

Verified by Experts

$tan A = 1 \Rightarrow \frac{B C}{A B} = 1 > B C = A B = K (say) .$
$∴ A C^{2} = (A B^{2} + B C^{2}) = (k^{2} + k^{2}) = 2 k^{2} \Rightarrow A C = \sqrt{2} k .$
$∴ sin A = \frac{B C}{A C} = \frac{k}{\sqrt{2} k} = \frac{1}{\sqrt{2}} .$
$∴ 2 sin A cos A = (2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}) = 1 .$

|

Updated on:21/07/2023

Class 10 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a right triangle ABC right-angled at B. if $t a n A = 1$ , then value of $2 sin A cos A = .$
A $0$
B $1$
C $2$
D $3$
Question 2 - Select One
In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
A $\frac{a^{2}}{b c}$
B $a + b$
C $\frac{b^{2}}{a c}$
D $\frac{c^{2}}{a b}$
Question 3 - Select One
In a triangle ABC right angled at B, the inradius r is equal to
A $c + b - a$
B $a + b + c$
C $\frac{a + c - b}{2}$
Dnone

RS AGGARWAL-TRIGONOMETRIC RATIOS-Exercise 10

Home
Ask Doubt
Profile