A company producing soft drinks has a contract which requires a minimum of 80 units of chemical A and 60 units of chemical B to go in each bottle of the drink. The chemicals are available in a prepared mix from two different suppliers.Suppleer X has a mix of 4 units of A and 2 units of B that costs Rs.10, and the supplier Y has a mix of 1 unit of A and 1 unit of B that costs Rs4. How many mixes from X and Y should the company purchase to honour the contract requirement and yet minimize the cost ?
The correct Answer is:10 mixes from X and 40 mixes form Y
To solve the problem, we need to formulate it as a linear programming problem and find the optimal solution. Here’s a step-by-step breakdown:
Step 1: Define the Variables
Let:
- x = number of mixes purchased from Supplier X
- y = number of mixes purchased from Supplier Y
Step 2: Define the Objective Function
We want to minimize the cost Z:
Z=10x+4y
where:
- 10x is the cost from Supplier X (Rs. 10 per mix)
- 4y is the cost from Supplier Y (Rs. 4 per mix)
Step 3: Define the Constraints
Based on the requirements for chemicals A and B, we can set up the following constraints:
1. For chemical A:
4x+1y≥80
2. For chemical B:
2x+1y≥60
3. Non-negativity constraints:
x≥0,y≥0
Step 4: Rewrite the Constraints
We can rewrite the constraints in a more standard form:
1. 4x+y≥80 (for chemical A)
2. 2x+y≥60 (for chemical B)
Step 5: Find the Intersection Points
To find the feasible region, we need to determine the points of intersection of the constraints.
1. From the first constraint 4x+y=80:
- If x=0: y=80 → Point (0, 80)
- If y=0: 4x=80 → x=20 → Point (20, 0)
2. From the second constraint 2x+y=60:
- If x=0: y=60 → Point (0, 60)
- If y=0: 2x=60 → x=30 → Point (30, 0)
3. Finding the intersection of the two lines:
- Set 4x+y=80 and 2x+y=60 equal to each other:
4x+y=80(1)
2x+y=60(2)
Subtract (2) from (1):
(4x+y)−(2x+y)=80−60
2x=20⇒x=10
Substitute x=10 into (2):
2(10)+y=60⇒20+y=60⇒y=40
So the intersection point is (10, 40).
Step 6: Identify the Feasible Region
The feasible region is bounded by the points:
- (0, 80)
- (20, 0)
- (0, 60)
- (30, 0)
- (10, 40)
Step 7: Evaluate the Objective Function at Each Vertex
Now we calculate Z at each vertex:
1. At (0, 80):
Z=10(0)+4(80)=320
2. At (20, 0):
Z=10(20)+4(0)=200
3. At (0, 60):
Z=10(0)+4(60)=240
4. At (30, 0):
Z=10(30)+4(0)=300
5. At (10, 40):
Z=10(10)+4(40)=100+160=260
Step 8: Determine the Minimum Cost
The minimum value of Z occurs at the point (10, 40):
Minimum cost=260
Conclusion
The company should purchase:
- 10 mixes from Supplier X
- 40 mixes from Supplier Y
Let:
- x = number of mixes purchased from Supplier X
- y = number of mixes purchased from Supplier Y
We want to minimize the cost Z:
Z=10x+4y
where:
- 10x is the cost from Supplier X (Rs. 10 per mix)
- 4y is the cost from Supplier Y (Rs. 4 per mix)
Based on the requirements for chemicals A and B, we can set up the following constraints:
4x+1y≥80
2. For chemical B:
2x+1y≥60
3. Non-negativity constraints:
x≥0,y≥0
We can rewrite the constraints in a more standard form:
1. 4x+y≥80 (for chemical A)
2. 2x+y≥60 (for chemical B)
To find the feasible region, we need to determine the points of intersection of the constraints.
- If x=0: y=80 → Point (0, 80)
- If y=0: 4x=80 → x=20 → Point (20, 0)
- If x=0: y=60 → Point (0, 60)
- If y=0: 2x=60 → x=30 → Point (30, 0)
- Set 4x+y=80 and 2x+y=60 equal to each other:
4x+y=80(1)
2x+y=60(2)
Subtract (2) from (1):
(4x+y)−(2x+y)=80−60
2x=20⇒x=10
Substitute x=10 into (2):
2(10)+y=60⇒20+y=60⇒y=40
So the intersection point is (10, 40).
The feasible region is bounded by the points:
- (0, 80)
- (20, 0)
- (0, 60)
- (30, 0)
- (10, 40)
Now we calculate Z at each vertex:
1. At (0, 80):
Z=10(0)+4(80)=320
2. At (20, 0):
Z=10(20)+4(0)=200
3. At (0, 60):
Z=10(0)+4(60)=240
4. At (30, 0):
Z=10(30)+4(0)=300
5. At (10, 40):
Z=10(10)+4(40)=100+160=260
The minimum value of Z occurs at the point (10, 40):
Minimum cost=260
The company should purchase:
- 10 mixes from Supplier X
- 40 mixes from Supplier Y
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXPRCISE 33B (LONG-ANSWER QUESTIONS)
3 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - SECTION A
4 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33A
11 Videos
- LINEAR DIFFERENTIAL EQUATIONS BOOK - RS AGGARWALCHAPTER - LINEAR DIFFERENTIAL EQUATIONS EXERCISE - Objective Questions
27 Videos
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F
21 Videos
Similar Questions
A company produces soft drinks that has a contract which requires that a minimum of 80 units of the chemical A and 60 units of the chemical B go into each bottle of the drink. The chemicals are available in prepared mix packets from two different suppliers. Supplier S had a packet of mix of 4 units of A and 2 units of B that costs Rs.10. The supplier T has a packet of mix of 1 unit of A and 1 unit of B costs Rs.4. How many packets of mixed from S and T should the company purchase to honour the contract requirement and yet minimize cost? Make a LPP and solve graphically.
View SolutionA company manufactures two types of chemicals A and B. Each chemical requires the types of raw materials P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.

The company gets profit of Rs. 350 and RS.400 by selling one unit of A and one unit of B respectively. If the entire production of A and B is sold, then formulate the problem as LPP.
View Solution
Knowledge Check
The unit of electro-chemical equivalent is
AgramBgram/ampereCgram/coulumbDcoulumb/gramThe unit of electro-chemical equivalent is
AgramBgram/ampereCgramlcoulumbDcoulumb/gramWhich of the following chemical units is certainly to be found in an enzyme?
A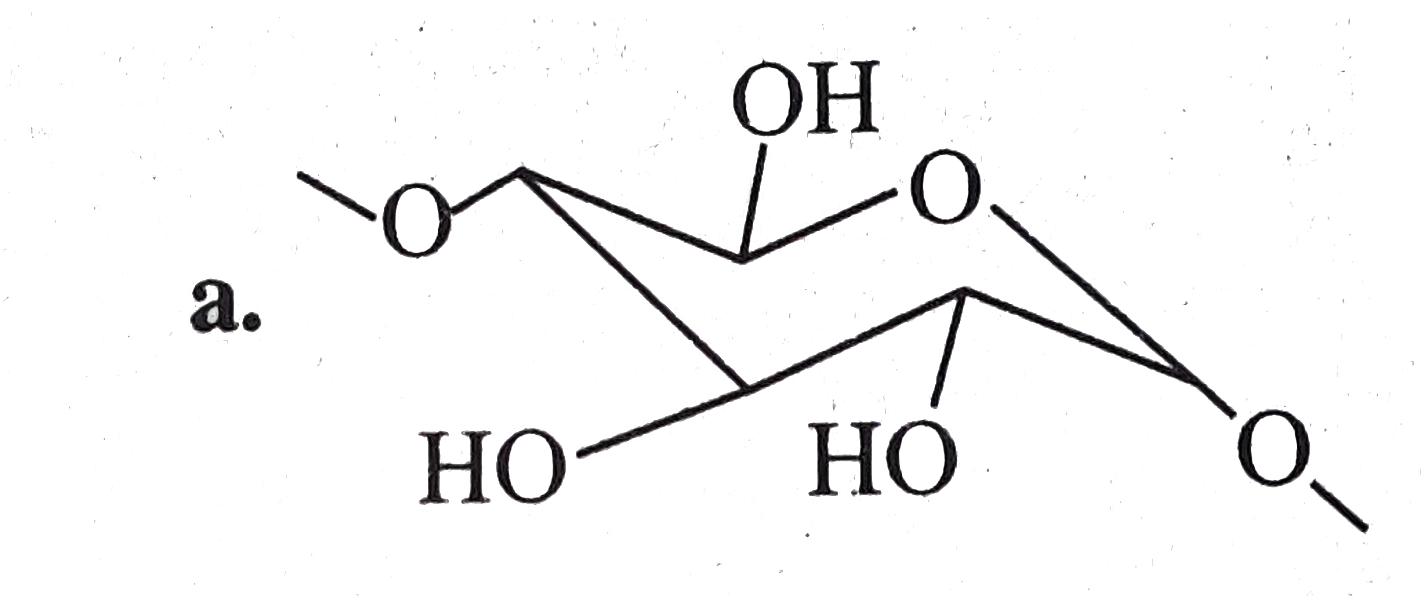 B
B C
C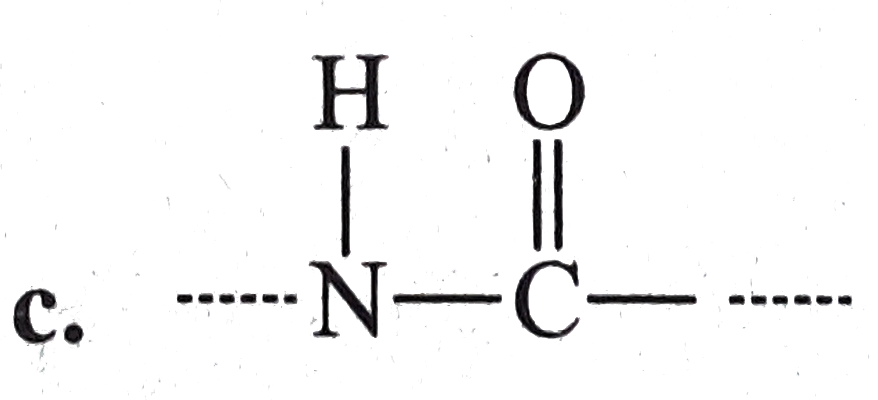 D
D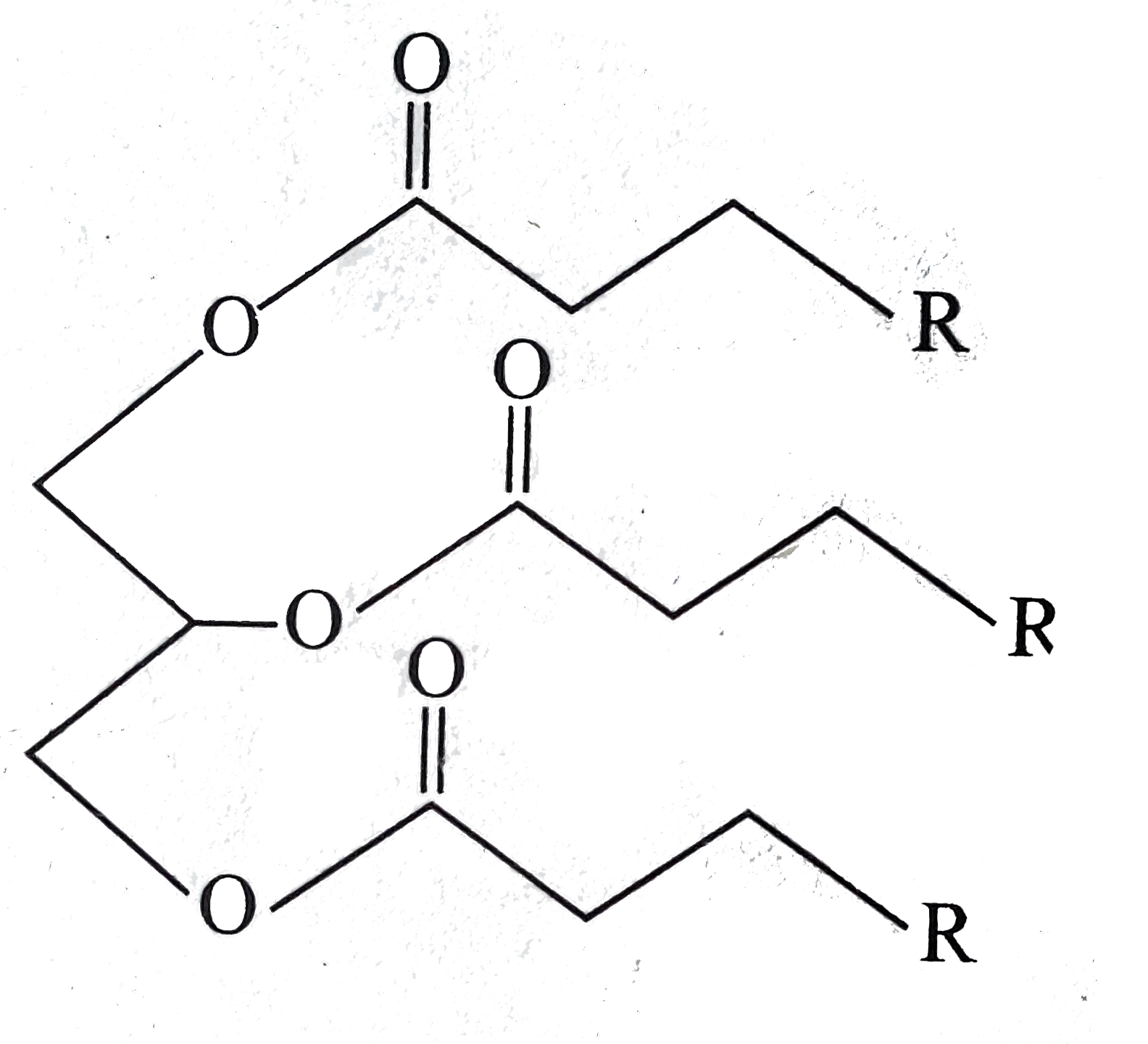
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2, are available. Food F1costs Rs 4 per unit food and F, costs Rs 6 per unit. One unit of food F1, contains 3 units of vitamin A and 4 units of minerals.One unit of foodF2,contains 6 units of vitamin A and 3 units of minerals.Formulate a LPP. find the minimum cost of diet which matches the minimal requirement
View SolutionA diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 units of calories. Two foods A and B are available at a cost of Rs. 5 and Rs. 4 per unit respectively. One unit of food A contains 200 units of vitamins, 1 unit of minerals and 40 units of calories whereas one unit of food B contains 100 units of vitamins, 2 units of minerals and 40 units of calories. Find what combination of the food A and B should be used to have least cost but it must satisfy the requirements of the sick person.
View SolutionWhich of the following chemical unit is certainly found in an enzyme?
View SolutionWhich one of the following chemical units is certainly to be found in enzymes ?
View SolutionWhich of the following has no units?
View Solution
