Doubtnut Promotions Sticky

Let E1={x∈R:x≠1 andxx−1>0} and E2={x∈E1:sin−1((log)e(xx−1)) is a real νmber} . Here, the inverse trigonometric function sin−1x assumes values in [π2,π2] . Let f:E1→R be the function defined by f(x)=(log)e(xx−1) and g:E2→R be the function defined by g(x)=sin−1((log)e(xx−1)) . LIST-I LIST-II P. The range of f is 1. (−∞,11−e]∪[ee−1, ∞) Q. The range of g contains 2. (0, 1) R. The domain of f contains 3. [12,12] S. The domain of g is 4. (−∞, 0)∪(0, ∞) 5. (−∞, ee−1] 6. (−∞, 0)∪(12,ee−1] The correct option is: P→4;  Q→2;  R→1;  S→1 (b) P→3;  Q→3;  R→6;  S→5 (c) P→4;  Q→2;  R→1;  S→6 (d) P→4;  Q→3;  R→6;  S→5

A

P→4,Q→2,R→1,S→1

B

P→3,Q→3,R→6,S→5

C

P→4,Q→2,R→1,S→6

D

P→4,Q→3,R→6,S→5

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

We have ,
E1={x∈R:x≠1andxx−1>0}
∴E1=xx−1>0
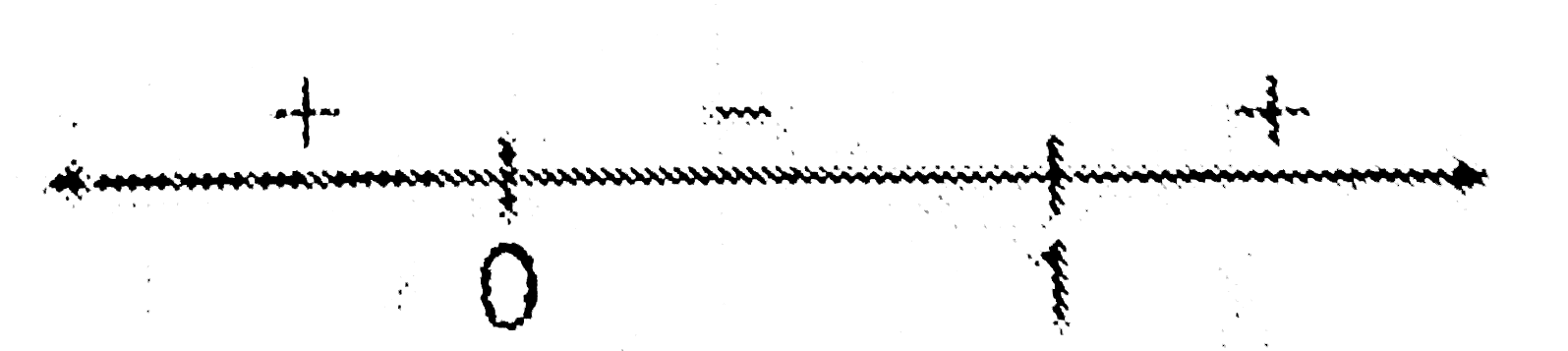
ocr_image
E1=x∈(−∞,0)∪(1,∞)
and
E2={x∈E1:sin−1(loge(xx−1)) is a real number }
E2=−1≤loge(x)x−1≤1⇒e−1≤xx−1≤e
Now, xx−1≥e−1⇒xx−1−1e≥0
⇒ex−x+1e(x−1)≥0⇒x(e−1)+1(x−1)e≥0
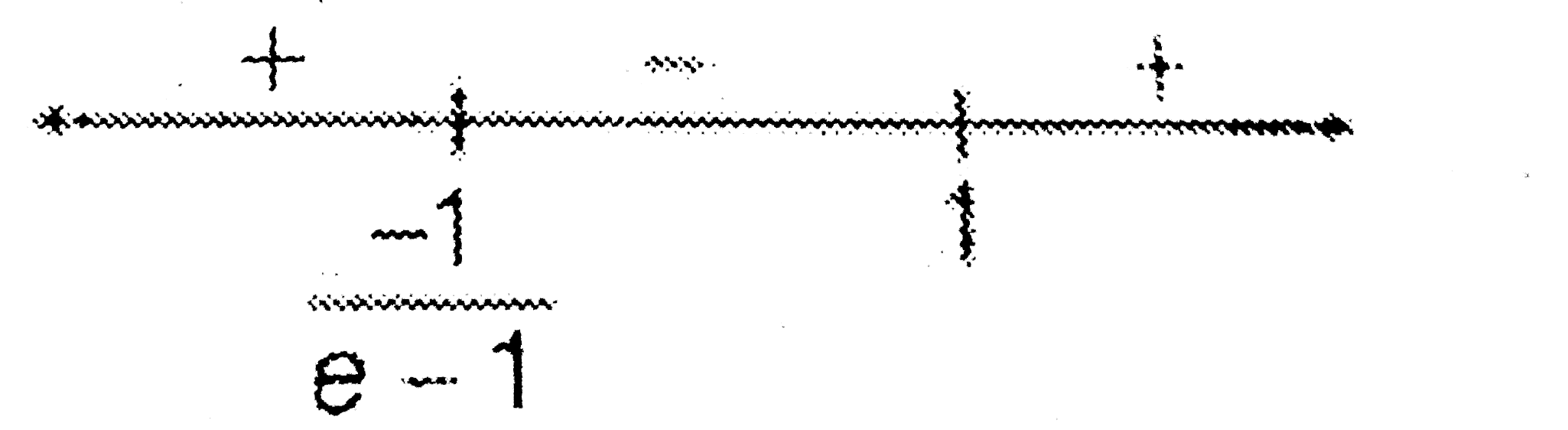
ocr_image
⇒x∈(−∞,11−e]∪(1,∞)
Also, xx−1≤e
⇒ (e−1)x−ex−1≥0
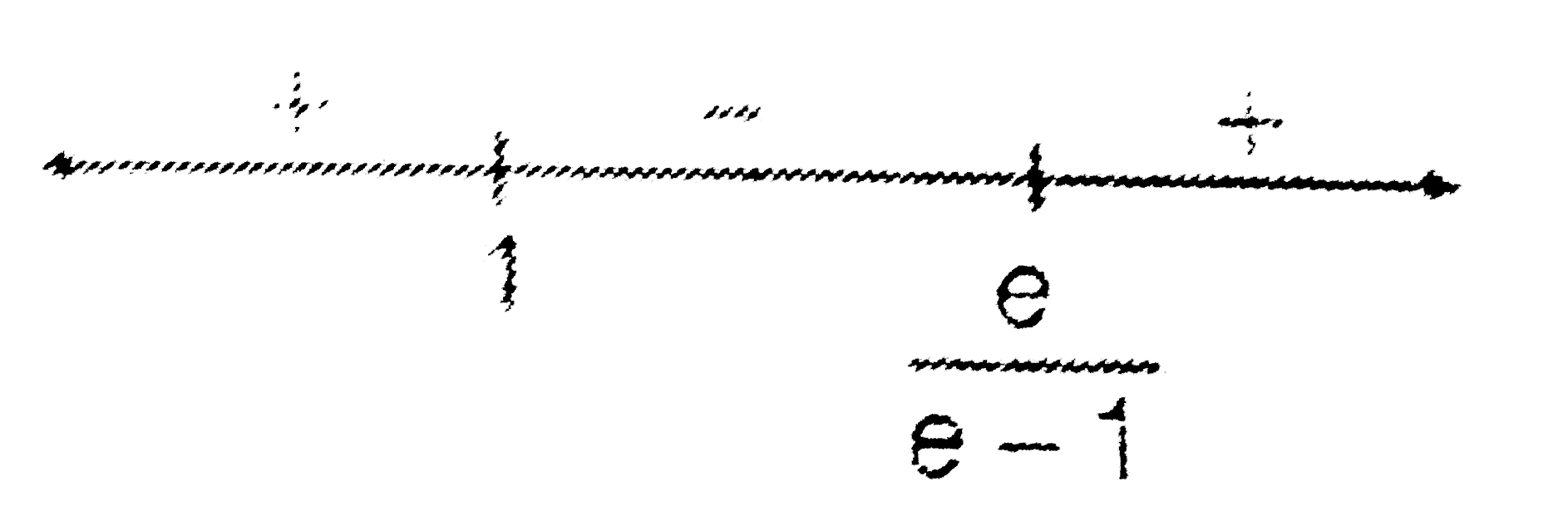
ocr_image
⇒x∈(−∞,1)∪[ee−1,∞)
So, E2=(−∞,11−e]m∪[ee−1,∞)
∴ The domain of f and g are
(−∞,11−e]∪[ee−1,∞)
and Range of xx−1 is R+−{1}
⇒ Range of f is R−{0}or(−∞,0)∪(0,∞)
Range of g is [−π2,π2]−{0}or[−π2,0)∪(0,π2]
Now, P→4,Q→2,R→1,S→1

|
Updated on:21/07/2023
Class 12MATHSFUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let E1={x∈R:x≠1andxx−1>0}andE2={x∈E1:sin−1(loge(xx−1)) is real number}
    (Here, the inverse trigonometric function sin−1x assumes values in [−π2,π2].)
    Let f:E1→R be the function defined by f(x)=loge(xx−1)andg:E2→R be the function defined by g(x)=sin−1(loge(xx−1)).
    ocr_image
    The correct option is

    Aa→s,b→q,c→p,d→p
    Ba→r,b→r,c→u,d→t
    Ca→s,b→q,c→p,d→u
    Da→s,b→r,c→u,d→t
  • Question 2 - Select One

    The domain of the function f(x)=sin−1log3(x3)) is

    A[1,9]
    B[−1,9]
    C[−9,1]
    D[−9,−1]