Consider the cube in the first octant with sides OP,OQ and OR of length 1, along the x-axis, y-axis and z-axis, respectively, where O(0,0,0) is the origin. Let S(12,12,12) be the centre of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST then the value of ∣∣(→p×→q)×(→r×(→t)∣is
The correct Answer is:(0.5)
(0.5) Here P(1,0,0) Q(0,1,0) R (0,0,1) , T =(1,1,1) and
S=(12,12,12)
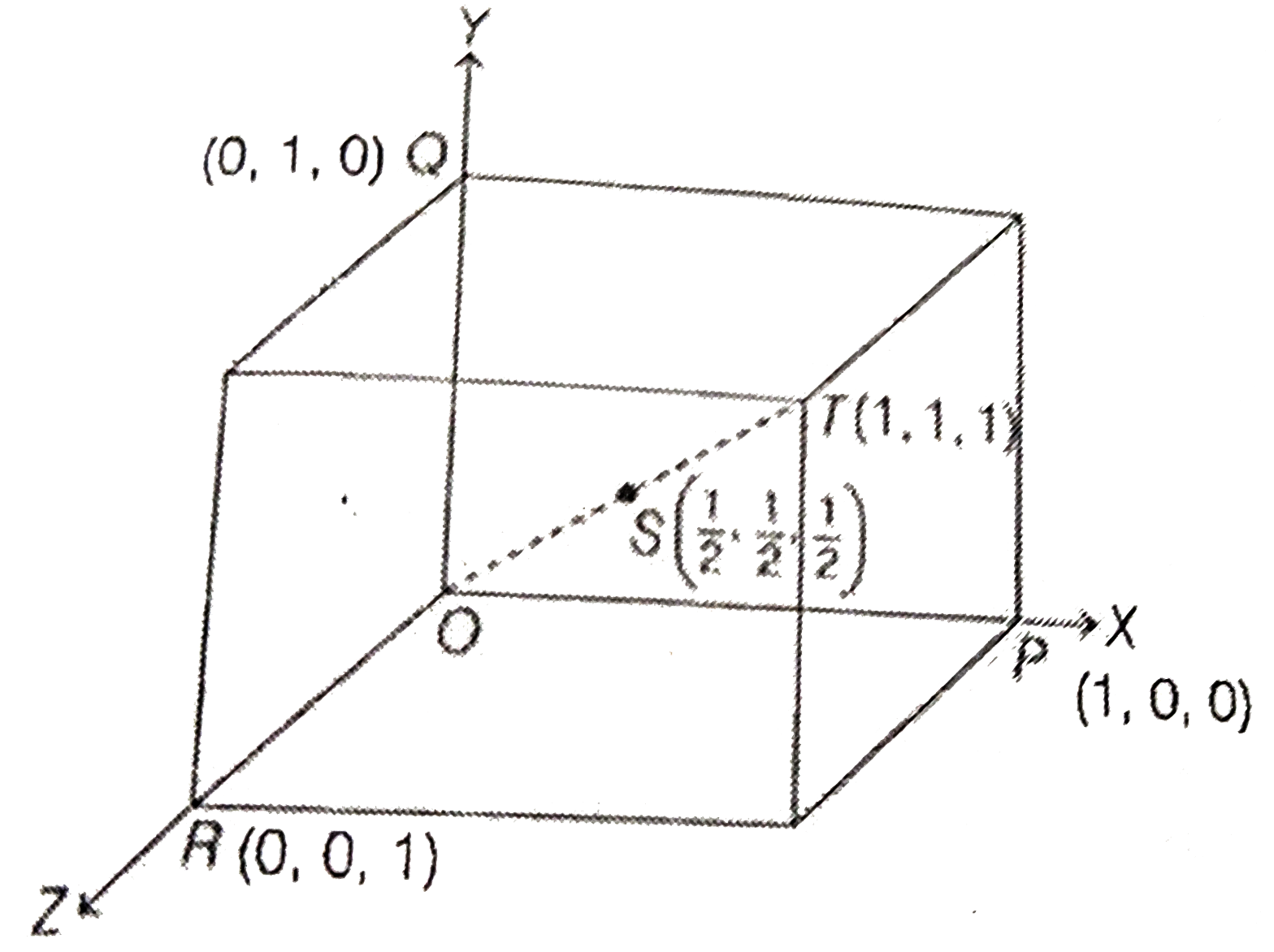
Now →P=−→SP=−−→OP−−−→OS
=(12ˆi−12ˆj−12ˆk)=12(ˆi−ˆj−ˆk)
→q=−−→SQ=12(ˆi+ˆj−ˆk)
→r=−−→SR=12(−ˆi−ˆj+ˆk)
And →t=−→ST=12(ˆi+ˆj+ˆk)
→p×→q=14∣∣
∣
∣∣ˆiˆjˆk1−1−1−11−1∣∣
∣
∣∣=14(2ˆi+2ˆj)
and→r×→t=14∣∣
∣
∣∣ˆiˆjˆk−1−11111∣∣
∣
∣∣=14(−2ˆi+2ˆj)
Now (→p×→q)×(→r×→t)=116∣∣
∣
∣∣ˆiˆjˆk222−220∣∣
∣
∣∣
=116(8ˆk)=12ˆk
∴(p×q)×(→r×→t)=∣∣∣12ˆk∣∣∣=12=0.5
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Vector Triple Product (Objective Questions II) (Fill in the Blank)1videos
VECTOR ALGEBRA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Vector Triple Product (Objective Questions II) (Analytical & Descriptive Questions)3videos
VECTOR ALGEBRA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Vector Triple Product (Objective Questions II)1videos
VECTOR ALGEBRA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL RATIOS AND IDENTITIESEXERCISE - HEIGHT AND DISTANCE10videos
TRIGONOMETRICAL RATIOS AND IDENTITIES
Similar Questions
A cube in the first octant has sides OP, OQ and OR of length 1, along the z-axis, y-axis and z-axis, respectively, where O(0, 0, 0) is the origin. Let the centre of the cube be at S(12.12,12) and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST, then the value of ∣∣(→p×→q)×(→r×→t)∣∣ is:
View SolutionIf →a=→p+→q,→p×→b=0and→q.→b=0, then prove that →b×(→a×→b)→b.→b=→q.
View Solution
Knowledge Check
- Question 1 - Select One
Let →p,→q,→r be three unit vectors such that →p×→q=→r. If →a is any vector such that [→a→q→r]=1,[→a→r→p]=2, and [→a→p→q]=3, then →a=
A→p+3q+→rB→3p+→2q+→rCvec(p)-vec(2q)-vec(3r)D→p+→2q+→3q - Question 2 - Select One
Let →a,→b and →c be three non-coplaner vectors and →p,→q,→r be three vectors such that →p=2→a−→b+→c,→q=→a−3→b+2→c,→r=→a+→b−→c. If [→a→b→c]=2 then [→p→q→r] equals
A6B-6C3DNone of these - Question 3 - Select One
On the xy plane where O is the origin, given points, A(1,0), B(0,1) and C(1,1). Let P,Q, and R be moving points on the line OA, OB, OC respectively such that −−→OP=45t(−−→OA),−−→OQ=60t(−−→OB),−−→OR=(1−t)(−−→OC) with t>0. If the three points P,Q and R are collinear then the value of t is equal to
A1106B7187C1100Dnone of these
OX, OY and OZ are three edges of a cube andn P,Q,R are the vertices of rectangle OXPY, OXQZ and OYSZ respectively. If vec(OX)=vecalpha, vec(OY)=vecbeta and vec(OZ)=vecgamma express vec(OP), vec(OQ), vec(OR) and vec(OS) in erms of vecalpha, vecbeta and vecgamma.
View SolutionP(→p)andQ(→q) are the position vectors of two fixed points and R(→r) is the position vectorvariable point. If R moves such that (→r−→p)×(→r−→q)=0 then the locus of R is
View SolutionLet →OA=→a,→OB=10→a+2→b,and→OC=bwhereO is origin. Let p denote the area of th quadrilateral OABCandq denote the area of teh parallelogram with OAandOC as adjacent sides. Prove that p=6q.
View SolutionLet O be the origin nad P, Q, R be the points such that −−→PO+−−→OQ=−−→QO+−−→OR. Then which one of the following is correct?
View SolutionThree vectors →P,→Q and →R are such that ∣∣→P∣∣,∣∣→Q∣∣,∣∣→R∣∣=√2∣∣→P∣∣ and →P+→Q+→R=0. The angle between →P and →Q,→Q and →R and →P and →Rare
View Solution

