t বেধের একটি সমান্তরাল পৃষ্টযুক্ত কাচ ফলকের উপরিতলে আলোকরশ্মি আপতিত হয়ে বিপরীত তল থেকে আপতিত রশ্মির সমান্তরালভাবে নির্গত হল। আপতন কোণ θ ক্ষুদ্র হলে প্রমান করো,পার্শ্বসরণ x=tθ(1−1μ), μ=কাচের প্রতিসরাঙ্ক।
Step by step video & image solution for t বেধের একটি সমান্তরাল পৃষ্টযুক্ত কাচ ফলকের উপরিতলে আলোকরশ্মি আপতিত হয়ে বিপরীত তল থেকে আপতিত রশ্মির সমান্তরালভাবে নির্গত হল। আপতন কোণ theta ক্ষুদ্র হলে প্রমান করো,পার্শ্বসরণ x=t theta(1-frac[1][mu]), mu=কাচের প্রতিসরাঙ্ক। by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- আলোর প্রতিসরণBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - আলোর প্রতিসরণEXERCISE - WBCHSE
20 Videos
- আলোর প্রতিসরণBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - আলোর প্রতিসরণEXERCISE - WBJEE
6 Videos
- আলোর প্রতিসরণBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - আলোর প্রতিসরণEXERCISE - NEET
4 Videos
- আলোর প্রতিফলন BOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - আলোর প্রতিফলন EXERCISE - EXERCISE
7 Videos
- আলোর বিচ্ছুরণ ও বিক্ষেপনBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - আলোর বিচ্ছুরণ ও বিক্ষেপনEXERCISE - EXAMPLE
5 Videos
Similar Questions
একটি পাত্রের উচ্চতা 15cm । এমনভাবে পাত্রে তরল ঢালা হল যেন পাত্রে তরলের তল পাত্রের ওপর থেকে 5cm নীচে থাকে। ওপর থেকে দেখলে মনে হয় তরলের তল অর্ধেক গভীরতায় আছে। তরলের প্রতিসরাঙ্ক কত?
View Solution10cm বেধের এবং 1.5 প্রতিসরাঙ্কবিশিষ্ট একটি কাচ ফলকের মধ্যে দিয়ে যেতে আলোর(শূন্যস্থানে আলোর গতিবেগ 3×108m⋅s−1) যে সময় লাগে, nanosecond এককে তা হল
View Solutionএকটি প্রিজমের নুন্যতম চ্যুতি কোণ এটির প্রতিসারক কোণের সাথে সমান হবে যদি প্রিজমটিকে এমন একটি পদার্থ দিতে বানানো হয় যার প্রতিসরাঙ্ক
View Solutionএকটি রশ্মি কোনো প্রতিফলকের সঙ্গে 50° কোণ করে আপতিত হয়| প্রতিফলনের ফলে রশ্মিটির চ্যুতি হবে
View Solutionমেঘ সাধারণত সাদা হয় কেন?
View SolutionShow that the unit of 1/sqrt(epsilon theta mu theta) is (m//s) .
View SolutionEffect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient μ. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
dN=(T+dT)sindθ2+Tsindθ2
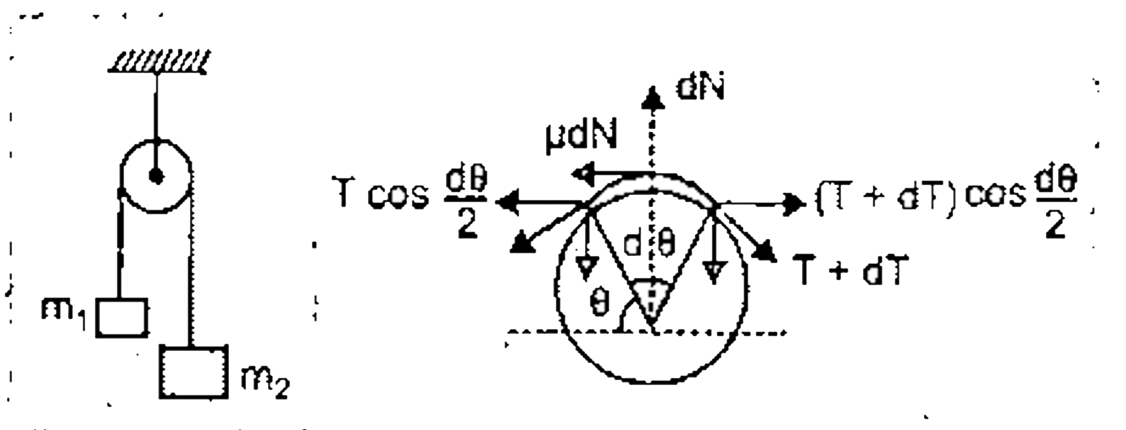
(T+dT)cosdθ2−Tcosdθ2−μdN=dra=0 (massless strings)
dTcosdθ2=μdN
dTcosdθ2=μ[(T+dt)sindθ2+Tsindθ2]
dt.cosdθ2=μ[Tsindθ2+dT.sindθ2+Tsindθ2]
dT=μ[T.dθ2+0+Tdθ2]=μTcosθ
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)<br>Supposecofficientofictionbetweenthestr∈gandp≤––––yismu =1/pi
What should be the ratio of heavier mass to lighter mass for no motion ?
View SolutionEffect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient μ. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
dN=(T+dT)sindθ2+Tsindθ2
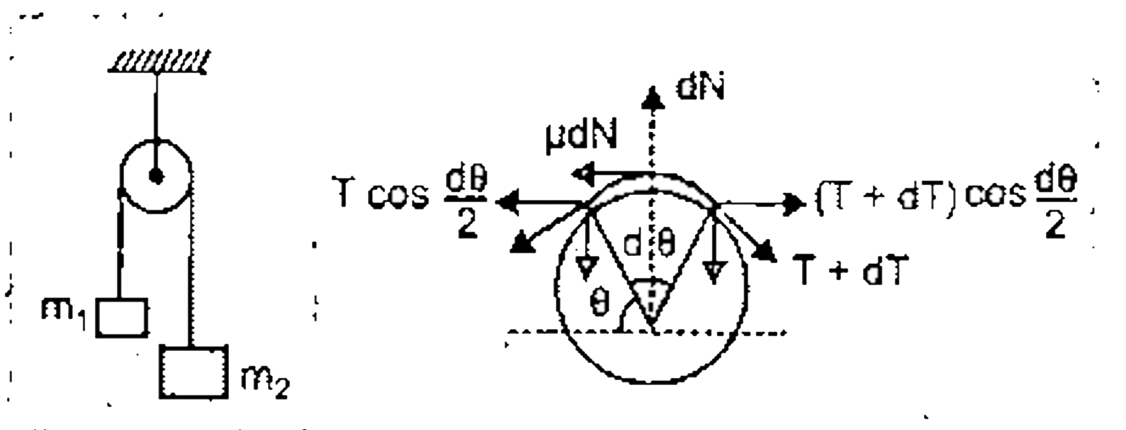
(T+dT)cosdθ2−Tcosdθ2−μdN=dra=0 (massless strings)
dTcosdθ2=μdN
dTcosdθ2=μ[(T+dt)sindθ2+Tsindθ2]
dt.cosdθ2=μ[Tsindθ2+dT.sindθ2+Tsindθ2]
dT=μ[T.dθ2+0+Tdθ2]=μTcosθ
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)<br>Supposecofficientofictionbetweenthestr∈gandp≤––––yismu =1/pi<br>Ifm_(2)=2em then acceleration of each mass is :
View SolutionEffect of friction between pulley and thread : In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient mu . Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string : dN=(T+dT) "sin" (d theta)/2+T "sin"(d theta)/2 (T+dT)"cos"(d theta)/2 -T"cos"(d theta)/2-mu dN=dr a=0 (massless strings) dT"cos"(d theta)/2=mu dN dT"cos"(d theta)/2=mu [(T+dt) "sin" (d theta)/2+T "sin" (d theta)/2] dt."cos" (d theta)/2=mu[T "sin" (d theta)/2+dT. "sin" (d theta)/2+T "sin" (d theta)/2] dT=mu[T. (d theta)/2+0+T(d theta)/2]=mu T cos theta int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi) Suppose cofficient of friction between the string and pulley is mu =1/pi The tension on side ofheavier\nass will be:
View SolutionEffect of friction between pulley and thread : In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient mu . Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string : dN=(T+dT) "sin" (d theta)/2+T "sin"(d theta)/2 (T+dT)"cos"(d theta)/2 -T"cos"(d theta)/2-mu dN=dr a=0 (massless strings) dT"cos"(d theta)/2=mu dN dT"cos"(d theta)/2=mu [(T+dt) "sin" (d theta)/2+T "sin" (d theta)/2] dt."cos" (d theta)/2=mu[T "sin" (d theta)/2+dT. "sin" (d theta)/2+T "sin" (d theta)/2] dT=mu[T. (d theta)/2+0+T(d theta)/2]=mu T cos theta int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi) Suppose cofficient of friction between the string and pulley is mu =1/pi The tension on side of lighter mass will be:
View SolutionThe distance from the line x=2+t,y=1+t,z=−12−12t to the plane x+2y+6z=10 is λ√μ. Then 5λ−μ=
View SolutionThe unit of 1/l√(T/μ)) is the same as that of (l-length, T-tension and μ-mass/unit length)
View Solution⎡⎢⎣0−tan(θ2)tan(θ2)0⎤⎥⎦ এবং I একটি 2×2ক্রমেরএককম্যাট্রিক্সহলে(I+A)(I-A)^-1 এর মান নির্নয় করো।
View SolutionA ray is incident at a small angle θ on a glass slab of thickness t. If the refractive index of glass is μ , show that the lateral displacement of the emergent ray from the slab is t θ(μ−1)/μ.
View Solution(i) Explain total internal reflection from law of refraction.
(ii) A ray of light is incident at a small angle θ on a rectangular glass slab of thickness t. If the refractive index of glass is μ . Show that the perpendicular distance between the emergent ray from the slab and the incident ray is tθ(μ−1)/μ .
View Solution
