A popular web video shows a jet airplane, a car, and a motorcycle racing from rest along a runway (Fig 2-10 ). Initially the motorcycle takes the lead, but then the jet takes the lead, and finally the car blows past the motorcycle. Here let's focus on the car and motorcycle and assign some reasonable values to the motion. The motorcycle first takes the lead because its ( constant) acceleration am=8.40m/s2 is greater than the car's ( constant) acceleration ac=5.60m/s2, but it soon loses to the car because it reaches its greater speed vm=58.8m/s before the car reaches the greatest speed vc=106m/s. How long does the car take to reach the motorcycle ?
Text Solution
KEY IDEA
We can apply the equations of constant acceleration to both vehicles, but for the motorcycle we must consider the motion in two stages: (1) First it travels through distance xml with zero initial velocity and acceleration am=8.40m/s2, reaching speed vm=58.8m/s. (2) Then it travels through distance xm2 with constant velocity vm=58.8m/s and zero acceleraton ( that, too, is a constant acceleraton). Note that we symbolized the distance even though we do not know their values, Symbolizing unknown quantities is often helpful in solving physics problems.)
Calculations: So that we can draw figures and do caculatons, let.s assume that the vehicles race along he positive direction of an x axis, starting from x=0 at time t=0. (We can choose any initial numbers because we are looking for the elapsed time, not a particular time in, say, the afternoon, but let.s stick with these easy numbers.) We

want the car to pass the motorcycle, but what does that mean mathematically ?
It means that at some time t, the side-by-side vehicles are at the same coordinate: xc for the car and the sum xm1+xm2 for the motorcycle. We can write this statement mathematically as
xc=xm1=xm2, (2-19)
Now let.s fill out both sides of Eq. 2-19, left side first. To reach the passing point at xc, the car accelerates from rest . From Eq. 2-15 (x−x0=v0t+12at2), with x0 and v0=0, we have
xc=12act2 (2-20)
To write an expression for xm1 for the motorcycle, we first find the time tm it takes to reach its maximum speed vm, using Eq. 2-11 (v=v0+at). Substituting v0=0,v=vm=58.8m/s, and a=am=8.40m/s2, that time is
tm=vmam=58.8m/s8.40m/s2=7.00s. (2-21)
To get the distance xm1 traveled by the motorcycle during the first stage, we again use Eq. 2-15 with x0=0 and v0=0, but we also substitute from Eq. 2-21 for the time. We find
xm1=12amt2m=12am(vmam)2=12v2mam. (2-22)
For the remaining time of t−tm, the motorcycle travels at its maximum speed with zero acceleration. To get the distance, we use Eq. 2-15 for this second stage of the motion, but now the initial velocity is v0=vm ( the speed at the end of the first stage) and the acceleration is a=0. So, the distance traveled during the second stage is
xm2=vm(t−tm)=vm(t−7.00s). (2-23)
To finish the calculation, we substitute Eqs. 2-20, 2-22, and 2-23 into Eq. 2-19, obtaining
12act2=12v2mam+vm(t−7.00s) (2-24)
This is a quadratic equation. Substituting in the given data, we solve the equation ( by using the usual quadratic-equation formula or a polynomial sovler on a calculator), finding t=44.4s and t=16.6s.
But what do we do with two answers? Does the car pass the motorcycle twice? No, of course not, as we can see in the video. So, one of the answers is mathematically correct but not physically meaningful. Because we know that the car passes the motorcycle after the motorcycle reaches its maximum speed at t=7.00s, we discard the solution with t<7.00s as being the unphysical answer and conclude that the passing occurs at
t=16.6s.
Figure 2-11 is a graph of the position versus time for the two vehicles, with the passing point marked. Notice that at t=7.00s the plot for the motorcycle switches from being curved ( because the speed had been increasing ) to being straight ( because the speed is thereafter constant).
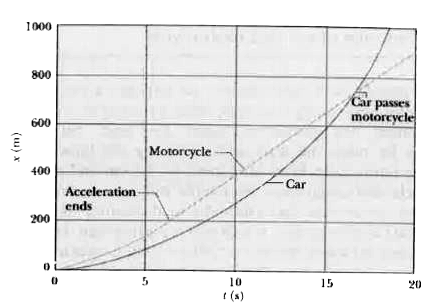
|
Topper's Solved these Questions
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - SAMPLE PROBLEM 2.08
1 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - SAMPLE PROBLEM 2.09
1 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - SAMPLE PROBLEM 2.06
1 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )
7 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
Similar Questions
Knowledge Check
Motorcycles are produced at
AFaridabadBBallbhgarhCMumbaiDBangaloreThe price of motorcycle depreciates every year by 8%. If the value of the motorcycle after 2 years will be Rs. 84640, then what is the present value (in Rs.) of the motorcycle?
A90000B102000C110000D100000What is the ratio of the total Demand of motorcycles of companies A and D taken together production of motorcycles of company D?
A13:9B8:5C5:3D9:7
The shortest distance between the car and the motorcycle if their initial positions are as shown, will be :
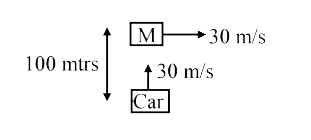
View SolutionThe shortest distance between the car and the motorcycle if their initial positions are as shown, will be :

View SolutionThere are 20 vehicles-cars and motorcycles in a parking area. If there are 56 wheels together, how many cars are there?
View SolutionA car and a motorcycle are moving with the same momentum. When equal retarding forces are applied, the car comes to halt in t1 seconds and the motorcycle in t2 seconds. If the mass of the car is five times more than the mass of the motorcycle then
View SolutionIn Q.107, after the car is overtaken by the motorycle, it will again overtake the motorcycle at what time, from t=0?
View Solution
