The shortest distance between the car and the motorcycle if their initial positions are as shown, will be :
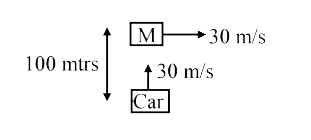
100 m
50√2
50 m
0 m
The correct Answer is:b
→VMC=→VMG−→VCG=30ˆI−30ˆj
tanθ=3030=1
→θ=45∘
shortest distance = cp=100sin45∘=50√2m

Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 1
75 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
Similar Questions
The shortest distance between the line x=y and the curve y2=x−2 is
View SolutionThe shortest distance between a diagonal of a unit cube and the edge skew to it, is
View SolutionThe shortest distance between IstandVth layer of HCP arrangement is:
View SolutionWhat will be the closest distance between the cars and also find the time instant at which the distance will be closest? :
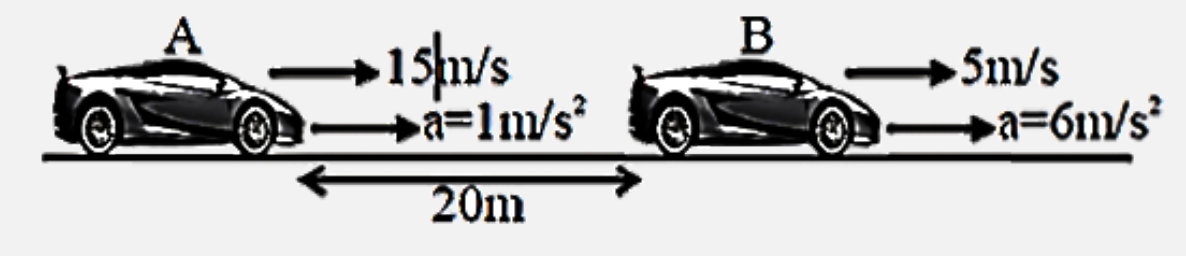 The distance will be:
The distance will be:
View SolutionStatement 1: The shortest distance between the lines x2=y−1=z2 and x−14=y−1−2=z−14 is √2. Statement 2: The shortest distance between two parallel lines is the perpendicular distance from any point on one of the lines to the other line.
View SolutionFind the shortest distance between the line y=x−2 and the parabola y=x2+3x+2
View SolutionThe shortest distance between the point (0,12) and the curve x=√y,(y>0) , is:
View SolutionFind the shortest distance between the line y=x−2 and the parabola y=x2+3x+2.
View SolutionFind the shortest distance between the line y=x−2 and the parabola y=x2+3x+2.
View SolutionFind the shortest distance between the line y=x−2 and the parabola y=x2+3x+2.
View Solution
