A football player, starting from rest at the line of scrimmage, accelerates along a straight line for a time of 1.5 s. Then , during a negligible amount of time, he changes the magnitude of his acceleration to a value of 1.1m/s2. With this acceleration, he continues in the same direction for another 1.2s, until he reaches a speed of 3.4 m/s. What is the value of his acceleration ( assumed to be constant ) during the initial 1.5 s period ?
0.91m/s2
1.1m/s2
1.4m/s2
2.2m/s2
The correct Answer is:C
To solve the problem step by step, we will break it down into two parts: the motion from point A to point B and the motion from point B to point C.
Step 1: Analyze the Motion from A to B
- The football player starts from rest, so the initial velocity u=0.
- The time taken to accelerate from A to B is tAB=1.5s.
- Let the acceleration during this time be a1.
- We can use the first equation of motion to find the velocity at point B:
vB=u+a1tAB
Substituting the known values:
vB=0+a1⋅1.5=1.5a1
Step 2: Analyze the Motion from B to C
- The player then accelerates with a new acceleration a2=1.1m/s2 for a time tBC=1.2s.
- The final velocity at point C is given as vC=3.4m/s.
- Using the first equation of motion again for the segment from B to C:
vC=vB+a2tBC
Substituting the known values:
3.4=1.5a1+1.1⋅1.2
Simplifying the equation:
3.4=1.5a1+1.32
Rearranging to solve for a1:
1.5a1=3.4−1.32
1.5a1=2.08
a1=2.081.5≈1.39m/s2
Conclusion
The value of the initial acceleration a1 during the first 1.5 seconds is approximately 1.39m/s2.
---
- The football player starts from rest, so the initial velocity u=0.
- The time taken to accelerate from A to B is tAB=1.5s.
- Let the acceleration during this time be a1.
- We can use the first equation of motion to find the velocity at point B:
vB=u+a1tAB
Substituting the known values:
vB=0+a1⋅1.5=1.5a1
- The player then accelerates with a new acceleration a2=1.1m/s2 for a time tBC=1.2s.
- The final velocity at point C is given as vC=3.4m/s.
- Using the first equation of motion again for the segment from B to C:
vC=vB+a2tBC
Substituting the known values:
3.4=1.5a1+1.1⋅1.2
Simplifying the equation:
3.4=1.5a1+1.32
Rearranging to solve for a1:
1.5a1=3.4−1.32
1.5a1=2.08
a1=2.081.5≈1.39m/s2
The value of the initial acceleration a1 during the first 1.5 seconds is approximately 1.39m/s2.
Topper's Solved these Questions
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( More than One Correct Choice Type )
6 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Linked Comprehension )
15 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PROBLEMS
53 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )
7 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
Similar Questions
A particle is moving along a straight line whose v-s graph is shown, the dashed line is tangent to the curve. The magnitude of acceleration is ( in m/s2)
View SolutionA motorcyclist starts from rest and reaches a speed of 6 m/s after travelling with uniform acceleration for 3 s. What is his acceleration ?
View Solution
Knowledge Check
An automobile starts from rest and accelerates to a final velocity in two stages along a straight road. Each stage occupies the same amount of time. In stage 1, the magnitude of the car's acceleration is 3.0m/s2. The magnitude of the car's velocity at the end of stage 2 is 2.5 times greater than it is at the end of stage 1. Find the magnitude of the acceleration is stage 2.
A4.5m/s2B3.0m/s2C3.8m/s2D2.2m/s2If acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
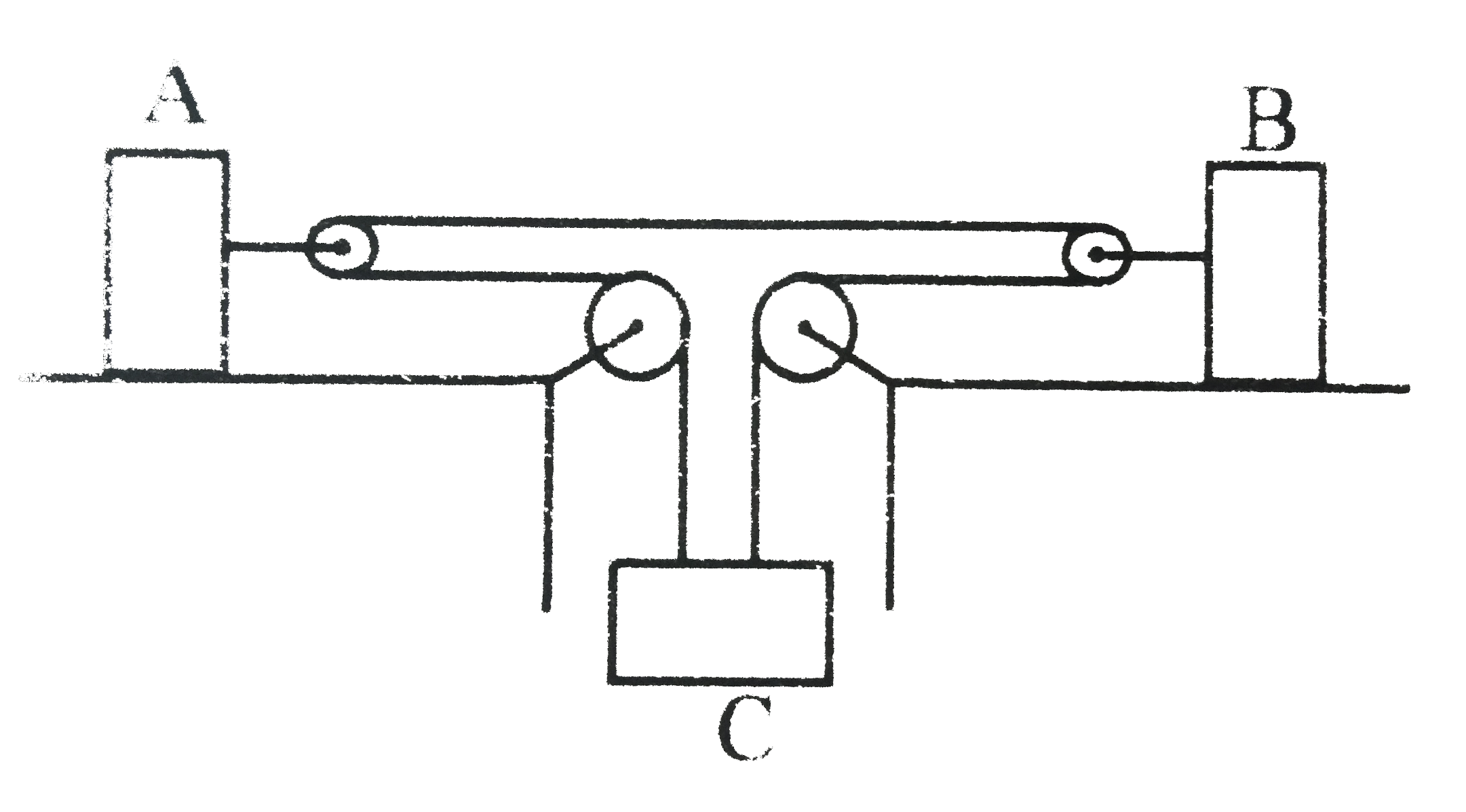 A1m/s2upwardsB1m/s2downwC2m/s2downwardsD2m/s2upwards
A1m/s2upwardsB1m/s2downwC2m/s2downwardsD2m/s2upwardsA body starts from rest and moves along a straight line path with uniform acceleration. The ratio of velocities at t = 1s and t = 2 s is ______.
A2:1B1:2C1:√2D√2:1
A particle starts from rest and moves with a constant acceleration along a straight path to attain 64 m s−1 in t s. If at t = (t + 3)s the speed is 76 ms−1, then find the acceleration of the particle and 't'.
View SolutionA car starts from rest and moves with uniform acceleration of 5 m/s2 for 8 sec. If the acceleration ceases after 8 seconds then find the distance covered in 12s starting from rest.
View SolutionAn object undergoes an acceleration of 8m/s2 starting from rest. Find the distance travelled in 1 second.
View SolutionA train starting from a railway station and moving with uniform acceleration attains a speed 40km/h in 10 minutes. Find its acceleration.
View SolutionA particle is moving with a uniform acceleration 4ms−2 for time 2 second and then 5ms−20 for time 3 seconds. What is the average acceleration of particle during motion.
View Solution
