A baseball is hit straight up and is caught by the catcher 2.0 s later, at the same height at which it left the bat. The maximum height of the ball during this interval is :
4.9 m
7.4 m
12.4 m
19.6 m
The correct Answer is:A
Topper's Solved these Questions
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( More than One Correct Choice Type )
6 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Linked Comprehension )
15 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PROBLEMS
53 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )
7 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
Similar Questions
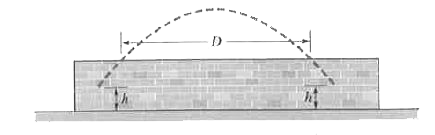
A baseball is hit at a height h = 1.00 m and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall. 4.00 s later, at distance D = 50.0 m farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and ( c) angle (relative to the horizontal) of the ball's velocity just after being hit? (d) How high is the wall?
View SolutionA ball thrown up verically returns to the thrower after 6 s. Find
(a) the velocity with which it was thrown up. (b) the maximum height it reaches, and (c ) its position after 4 s.
View Solution
Knowledge Check
When a ball is thrown up vertically with velocity u, it attains a maximum height H. What should be the velocity so that maximum height becomes 2H?
A√2uB2uC3uDu√2A ball of mass 50 g is dropped from a height of 20 m. A boy on the ground hits the ball vertically upwards with a bat with an average force of 200 N, so that it attains a vertical height of 45 m. The time for which the ball remains in contact with the bat is [Take g=10m/s2]
A1/10th of a secondB1/40th of a secondC1/80th of a secondD1/120∘ of a secondA ball of mass 50 g is dropped from a height of 20 m. A boy on the ground hits the ball vertically upwards with a bat with an average force of 200 N, so that it attains a vertical height of 45 m. The time for which the ball remains in contact with the bat is [Take g=10m/s2]
A1/20th of a secondB1/40th of a secondC1/8oth of a secondD1/20th of a second
You throw a baseball straight upward. If air resistance is not neglected, how does the time required for the ball to.go, from the height at which it was thrown up to its maximum height compare to the time required for it to fall from its maximum height back down to the height from which it was thrown ? Explain your answer.
View SolutionIn a cricket match, a batsman hits the ball in air. A fielder, originally standing at a distance of 12 m due east of the batsman, starts running 0.6 s after the ball is hits. He runs towards north at a constant speed of 5m/s and just manages to catch the ball 2.4 s after he starts running. Assume that the ball was hit and caught at the same height and take g=10m/s2g=10m/s2 Find the speed at which the ball left the bat and the angle that its velocity made with the vertical.
View SolutionIn quick succession, a large number of balls are thrown up vertically in such a way that the next ball is thrown up when the previous ball is at the maximum height. If the maximum height is 5m, then find the number of the balls thrown up per second (g=10 m s^(-2)).
View SolutionA ball of mass 50 g is dropped from a height of 20 m. A boy on the ground hits the ball vertically upwards with a bat with an average force of 200 N, so that it attains a vertical height of 45 m. The time for which the ball remains in contact with the bat is [Take g=10m/s2]
View SolutionA boy throws n balls per second at regular time intervals. When the first ball reaches the maximum height he throws the second one vertically up. The maximum height reached by each ball is
View Solution
