The minimum takeoff speed for a certain airplane in 75 m/s. What minimum acceleration is requied if the plane must leave a runway of length 950 m ? Assume the plane starts from rest at one end of the runway .
, upward
, upward
, downward
, downward
The correct Answer is:C
To solve the problem of finding the minimum acceleration required for an airplane to take off from a runway of length 950 m, given that its minimum takeoff speed is 75 m/s and it starts from rest, we can use the equations of motion.
1. Identify the Given Values:
- Initial velocity (u) = 0 m/s (the plane starts from rest)
- Final velocity (v) = 75 m/s (minimum takeoff speed)
- Displacement (s) = 950 m (length of the runway)
2. Use the Equation of Motion:
We can use the third equation of motion, which relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
3. Substitute the Known Values:
Plugging in the known values into the equation:
(75)2=(0)2+2a(950)
4. Calculate v2:
752=5625
So, the equation becomes:
5625=2a(950)
5. Simplify the Equation:
5625=1900a
6. Solve for Acceleration (a):
a=56251900
a≈2.9684m/s2
7. Round the Result:
The minimum acceleration required is approximately:
a≈2.97m/s2
This can be rounded to 3 m/s² for practical purposes.
Final Answer:
The minimum acceleration required for the airplane to take off is approximately 3 m/s².
---
- Initial velocity (u) = 0 m/s (the plane starts from rest)
- Final velocity (v) = 75 m/s (minimum takeoff speed)
- Displacement (s) = 950 m (length of the runway)
We can use the third equation of motion, which relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
Plugging in the known values into the equation:
(75)2=(0)2+2a(950)
752=5625
So, the equation becomes:
5625=2a(950)
5625=1900a
a=56251900
a≈2.9684m/s2
The minimum acceleration required is approximately:
a≈2.97m/s2
This can be rounded to 3 m/s² for practical purposes.
The minimum acceleration required for the airplane to take off is approximately 3 m/s².
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( More than One Correct Choice Type )6videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Linked Comprehension )15videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PROBLEMS53videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
What is the minimum length of a plane mirror required for a person of height 2m to see his full image? Is there any restriction on the position of the top edge of the mirror?
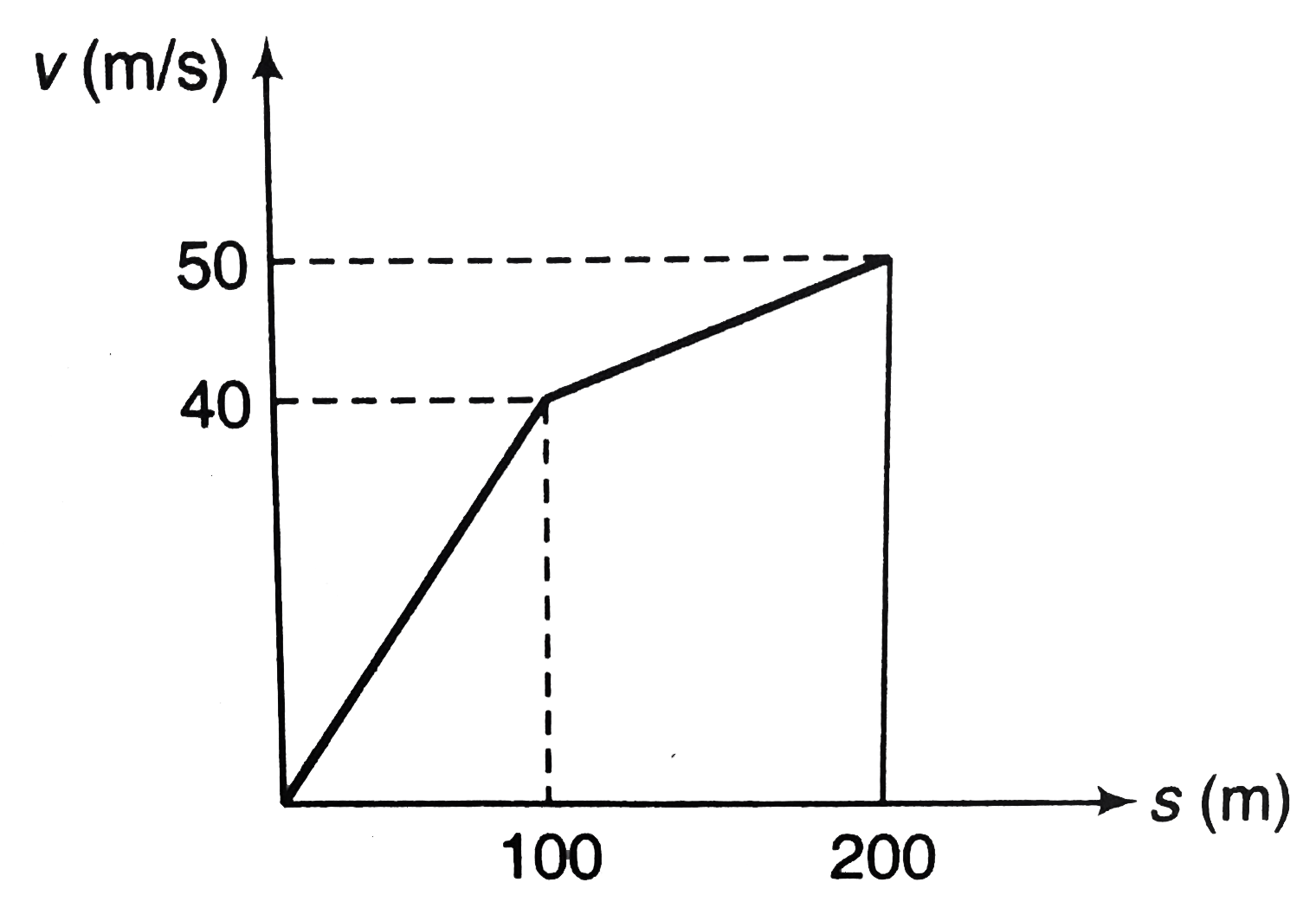
View SolutionThe v-s graph for an airplane travelling on a straight runway is shown. Determine the acceleration of the plane at s=50m and s=150m. Draw the a-s graph.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The acceleration a of a particle in ms2 is give by a=18t2+36t+120. If the particle starts from rest, then velocity at end of 1 s is
A122 m/sB140 m/sC144 m/sD120 m/s - Question 2 - Select One
A car accelerates from rest with acceleration 1.2m/s2. A bus moves with constant speed of 12 mis in a parallel lane. How long does the car take from its start to meet the bus?
A17 sB8 sC20 sD12 s
The minimum velocity required to complete a full circle in a vertical plane is given to a bob of mass m suspended by a string of length 25 cm. When it reaches the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. After the collision, if the second bob acquires the minimum speed required to complete a full circle in the vertical plane, then the length of the string l2 __m. (Both the strings are massless and in-extensible)
View SolutionIn the arrangement shown in the figure, the block C begins to move down at a constant speed of 7.5cm/s at time t=0. At the same instant block A is made to start moving down at constant acceleration. It starts at M and its speed is 30cm/s when it reaches N(MN=20cm). Assuming that B started from rest, find its position, velocity and acceleration when block A reaches N.
 View Solution
View SolutionThe velocity-displacement for a fer plane on a straight runway is shown in . Determine the speed and acceleration of the jet plane at s=150m.
 .View Solution
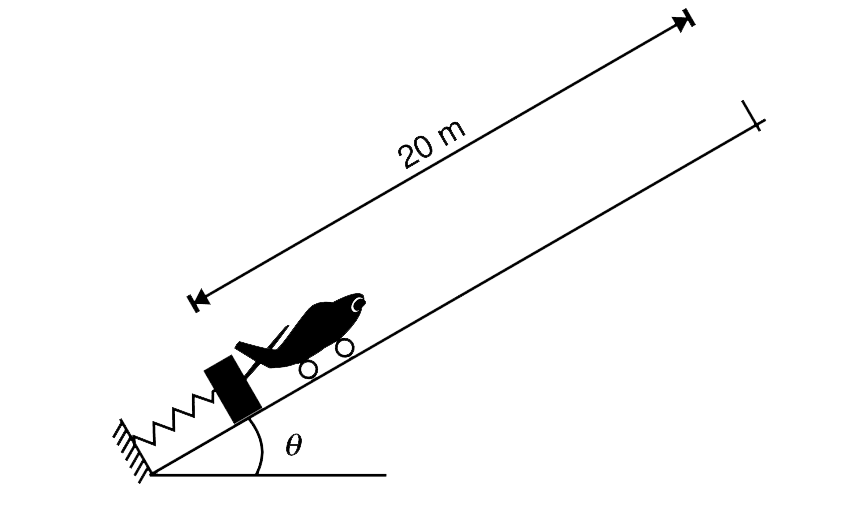
.View SolutionIn an aircraft carrier warship the runway is a 20 m long strip inclined at θ=20∘ to the horizontal. The launcher is effectively a large spring that pushes an aircraft of mass m = 2000 kg for first 5 m of the 20 m long runway. The jet engine of the plane produces a constant thrust of 6×104N for the entire length of the runway. The plane needs to have a speed of 180 kph at the end of the runway. Neglect air resistance and calculate the spring constant of the launcher. [sin20∘=0.3 and g=10m/s2]
 View Solution
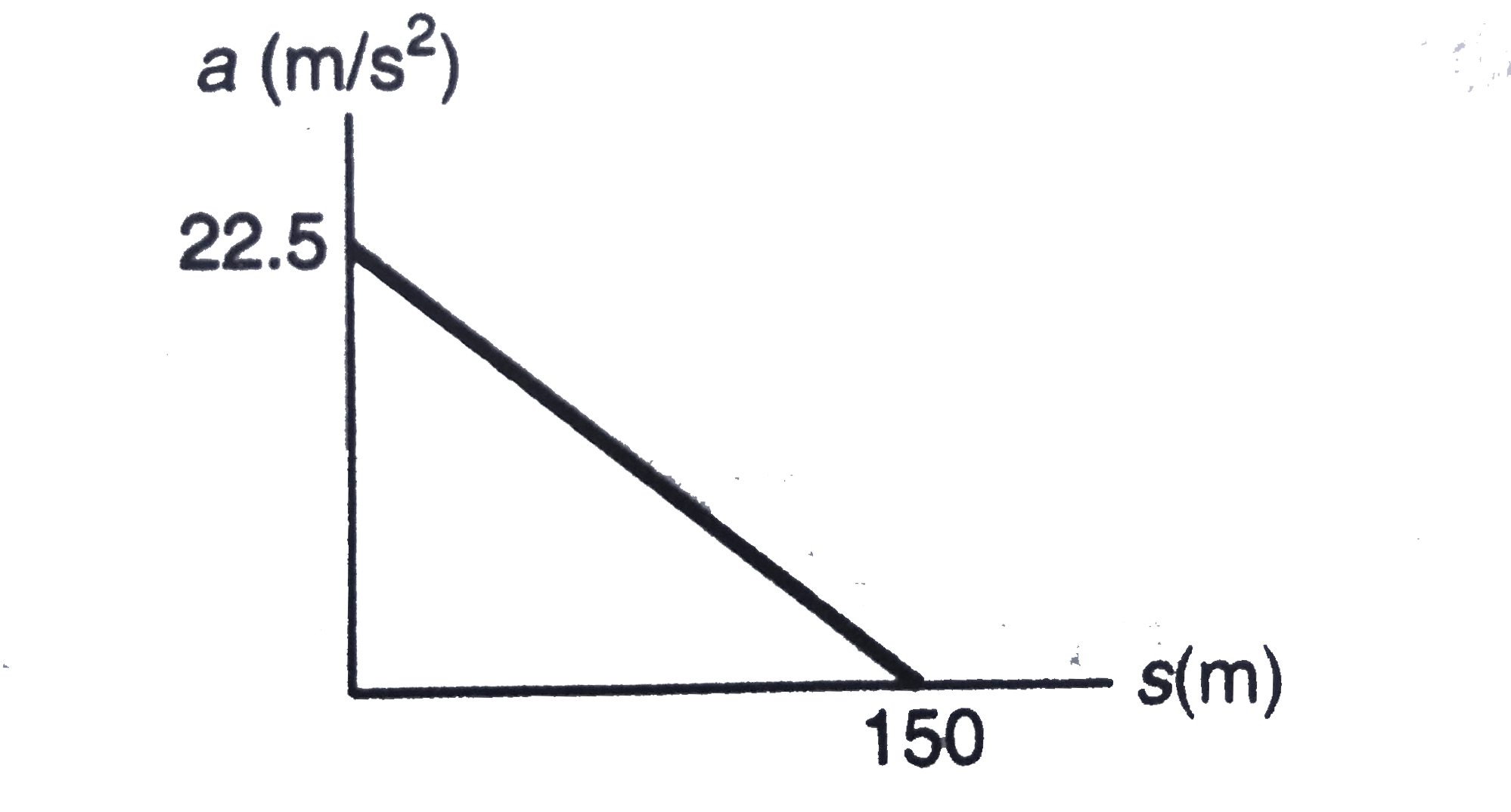
View SolutionThe jet plane starts from rest at s=0 and is subjected to the acceleration shown. Determine the speed of the plane when it has travelled 60 m.
 View Solution
View SolutionOne end of a light rod is clamped in such a manner that rod can be rotated in a vertical plane . A block of mass mis attached to the other ened of rod and the block stays at rest at its lowest position . What minimum speed should be imparted to the bock so that it may complete its circle ? Assume length of rod to be l .
View Solution

