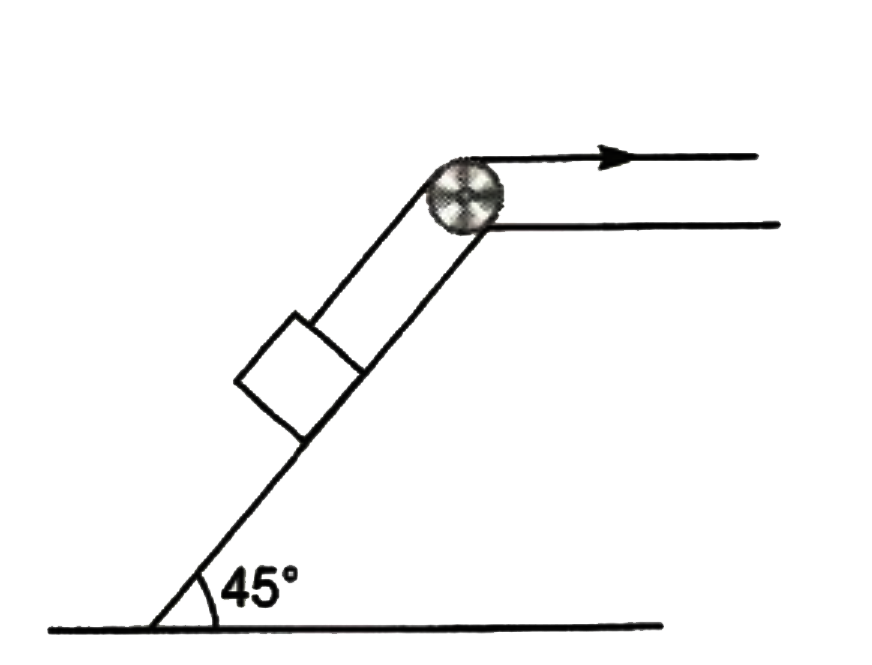
A block of mass 200kg is being pulled by mean on an inclined plane at angle of as shown. The coefficient of static friction of 0.5. Each man can only apply a maximum force of 500N. The number of men required for the block to just start moving up the plane is

Because the block is on the verge of moving, the static frictional force must be at its maximum possible value, that is, . (2) Because the block is on the verge of moving up the plane, the frictional force must be down the plane (to oppose the pending motion). (3) From Sample Problem 5.05, we know that the component of the gravitational force down the plane is and the component perpendicular to (and inward from the plane is (Fig. 6-11b).
Calculations: Figure 6-11c is a free-body diagram for the block, showing the force applied by the ropes, the static frictional force , and the two components of the gravitational force. We can write Newton.s second law for forces along the x axis as
Because the block is on the verge of sliding and the frictional force is at the maximum possible value we use Eq. 6-1 to replace with :
From Fig. 6-11c, we see that along the y axis Newton.s second law becomes
.
Solving Eq. 6-21 for and substituting the result into Eq. 6-20, we have
.
Substituting this expression into Eq.6-19 and solving for F lead to
Substituting , we find the stone block on the verge of moving is . Dividing this by the assumed pulling force of 686 N from each man, we find that the required number of men is
men.
Comment: Once the stone block began to move, the friction was kinetic friction and the coefficient was about 0.20. You can show that the required number of men was then 26 or 27. Thus, the huge stone blocks of the Great Pyramid could be pulled up into position by reasonably small teams of men.

Figure 6-11 (a) A stone block on the verge of being pulled up the side of the Great Pyramid. (b) The components of the gravitational force. (c) A free-body diagram for the block.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS5videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
A block of mass 200 kg is being pulled by some men, up an inclined plane of inclination 45∘ and coefficient of friction 0.5, as shown in the figure. If the figure. If each man can apply a maximum number of men required to just slide the block, up the plane is
 View Solution
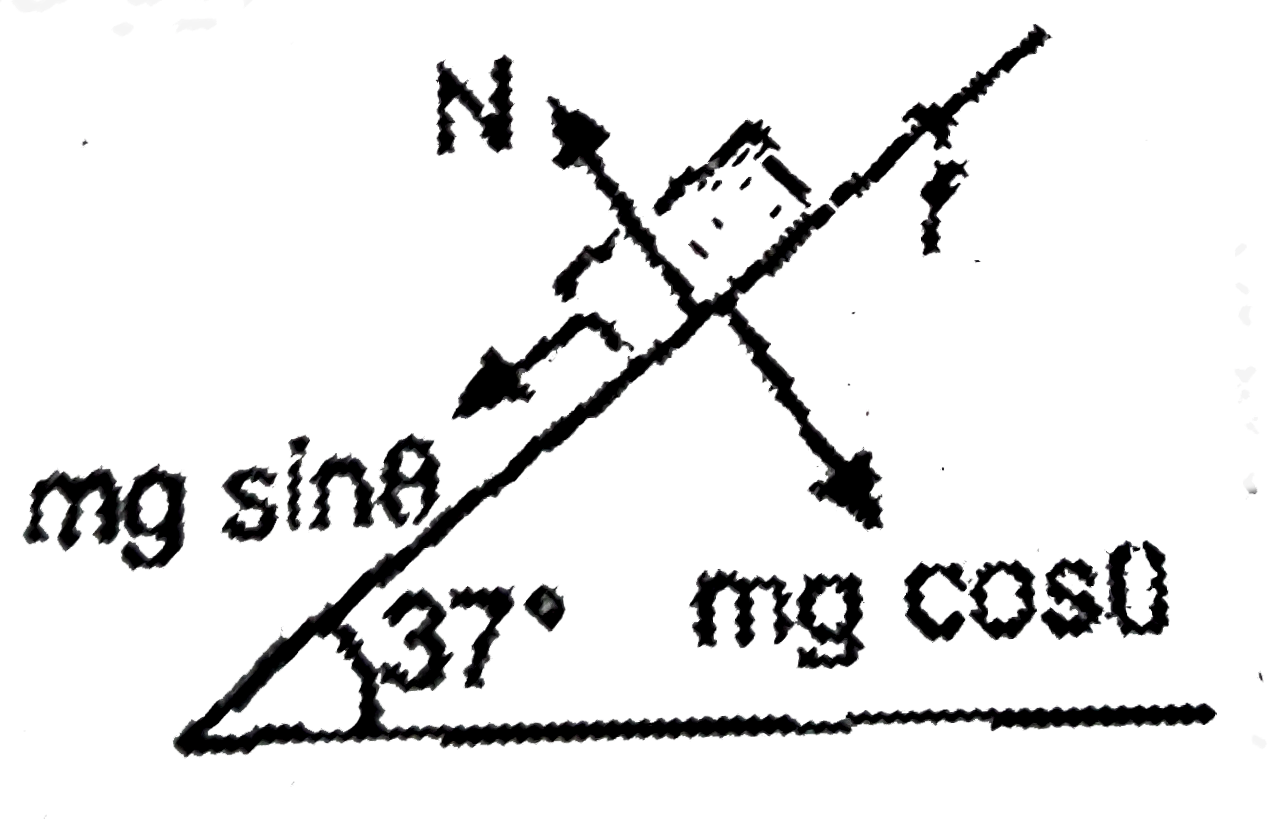
View SolutionA block of mass 3 kg slides on a rough fixed inclined plane of 37∘ angle having coefficient of friction 0.5. find the resultant force exerted by plane on the block.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8N - Question 2 - Select One
A block rests on an inclined plane that makes an angle with the horizontal, if the coefficient of sliding friction is 0.50 and that of static friction is 0.75, the time required to slide the block 4 m along the inclined plane is -
A25sB10sC5sD2s - Question 3 - Select One
A body of mass 10 kg is lying on a rough plane inclined at an angle of 30∘ to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane is
A914 NB91.4 NC9.14 ND0.914 N
A block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
 View Solution
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
 View Solution
View SolutionA body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
View SolutionA block of mass 10 kg is placed on an inclined plane when the angle of inclination is 30∘. The block just begins to slide down the plane. The force of static friction is
View Solution

