Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
-4
−3225
3225
4
The correct Answer is:B, D
Step by step video, text & image solution for Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities rho_1 and rho_2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio rho_1/rho_2 can be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION -3)
5 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I: PHYSICS (SECTION-1) (One or more options correct Type)
9 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION -1)
10 Videos
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
Similar Questions
Two non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ respectively are placed such that they partially overlapping region.
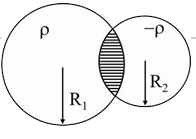
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View Solution
Knowledge Check
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
AAR8ε0BAR4ε0CARε0DAR2ε0A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
AIncreases as r increases inside the sphereBDecreases as r increases inside as well as outsideCIncreases as increases outside the sphereDIs discontinuousat r=RA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
A(a) increases as r increases, for r<R.B(b) decreases as r increases, for 0<r<∞.C(c) decreases as r increases, for R<r<∞.D(d) is discontinuous at r=R.
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionTwo conducting spheres of radii r1 and r2 are charged to the same surface charge density . The ratio of electric field near their surface is
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View Solution
