A nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

ρ3ε0→d
ρ3ε0(→r−→d)
ρ3ε0(→d−→r)
ρ3ε0(→r)
The correct Answer is:C
−→EP=−ρ3ε0→s=−ρ3ε0(→r−→d)
=ρ3ε0(→d−→r)

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
There is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View SolutionA sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>R - Question 2 - Select One
A solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
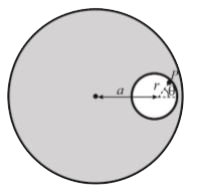 A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa - Question 3 - Select One
An insulated sphere of radius R has a uniform volume charge density λ. The electric field at a point A, which is at distance r from its center is given by (R>r)
AZeroBRλ/3∈0C2rλ3∈0Drλ3∈0
A sphere of radius 2R has a uniform charge density p. The difference in the electric potential at r = R and r = 0 from the centre is:
View SolutionA solid sphere of radius R is charged with volume charge density p=Krn , where K and n are constants and r is the distance from its centre. If electric field inside the sphere at distance r is proportional to r4 ,then find the value of n.
View SolutionA solid non conducting sphere of radius R and uniform volume density ρ has centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R, 0, 0) (ii) (0, 0, R/2) (iii) (R, R, R)View SolutionAn insulated sphere of radius r haas a uniform volume charge density λ. The electric field at a point A, which is at distance r from its centre is given by (R>r)
View SolutionThere is a solid non-conducting sphere of radius R. Sphere is uniformly charged over the volume. Electric field due to this where in observed.
View Solution

