Consider two solid spheres P and Q each of density 8gmcm−3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gmcm−3 and viscosity η=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm−3 and viscosity η=2 poiseulles. The ratio of the terminal velocities of P and Q is
Step by step video & image solution for Consider two solid spheres P and Q each of density 8gm cm^-3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gm cm^-3 and viscosity eta=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm^-3 and viscosity eta=2 poiseulles. The ratio of the terminal velocities of P and Q is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION 1)13videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION 3)2videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART-1 PHYSICS (SECTION 2 )8videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 36videos
JEE (ADVANCE) 2020
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-36videos
JEE ADVANCED 2020
Similar Questions
The electrostatic energy of Z protons uniformly distributed throughout a spherical nucleus of radius R is given by
E=3Z(Z−1)e25(4πe0R)
The measured masses of the neutron _(1)1H,157Nand,168Oare1.008665u,1.007825u,15.000109uand15.003065u, respectively Given that the ratio of both the _(7)12N and _(8)15O nucleus are same , 1 u = = 931.5 Me Vc2 (c is the speed of light ) and e2/(4πe0)=1.44MeV fm Assuming that the difference between the binding energies of _715Nand_(8)^(15) O is purely due to the electric energy , The radius of the nucleus of the nuclei is12:44View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
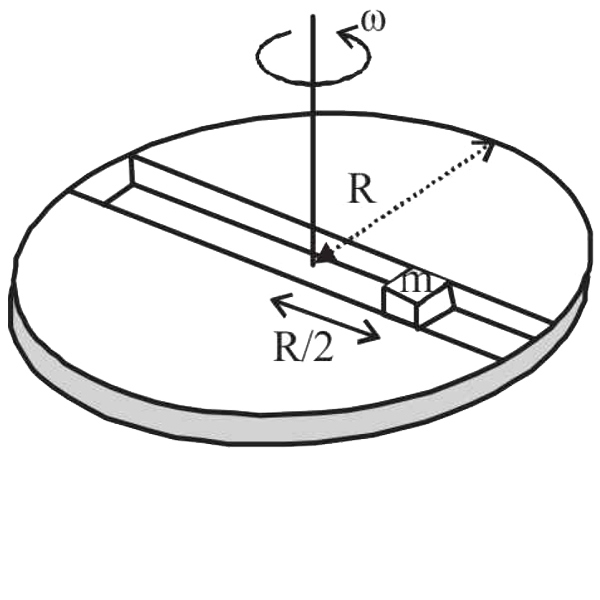
The distance r of the block at time is05:17View SolutionHighly excited states for hydrogen like atoms (also caleld Rydberg states) with nuclear charge Ze are degined by their orbit number n, where n>>1. Which of the following statement (s) is (are) true?
03:53View SolutionA spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
02:49View SolutionPut a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
05:05View SolutionTwo spheres P and Q of equal radii have densities rho_1 and rho_2 , respectively. The spheres are connected by a massless string and placed in liquids L_1 and L_2 of densities sigma_1 and sigma_2 and viscosities eta_1 and eta_2 , respectively. They float in equilibrium with the sphere P in L_1 and sphere Q in L_2 and the string being taut(see figure). If sphere P alone in L_2 has terminal velocity vecV_p and Q alone in L_1 has terminal velocity vecV_Q , then
11:10View SolutionConsider two solid spheres P and Q each of density 8gm cm^-3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gm cm^-3 and viscosity eta=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm^-3 and viscosity eta=2 poiseulles. The ratio of the terminal velocities of P and Q is
01:31View SolutionA lead sphere of 1.0 mm diameter and relative density 11.20 attains a terminal velocity of 0.7 cm s^(-1) in a liquid of relative density 1.26 . Determine the coefficient of dynamic viscosity of the liquid.
06:12View SolutionA sphere of radius R and density rho_1 is dropped in a liquid of density sigma . Its terminal velocity is v_1 . If another sphere of radius R and density rho_2 is dropped in the same liquid, its terminal velocity will be:
03:02View SolutionWhen 100 drops of a liquid P is added into a liquid Q the volume of the liquid in the container which is initially filled with liquid Q doubled. Determined density of the mixture if density of the liquids P and Q are 1.5 g cm ^(-3) and 1.3 g cm^(-3), respectively
02:02View SolutionA hollow sphere of external and internal diameter 4 cm and 2 cm, respectively, floats in a liquid of density 3.5 g cm−3. The level of the liquid coincides with the center of the sphere. Calculate the density of the material of the sphere.
02:36View SolutionA sphere of radius R is gently dropped into liquid of viscosity η in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2 R when dropped into the same liquid, will attain its teriminal velocity.
03:33View Solution8 ग्राम/सेमी3 घनत्व वाले दो ठोस गोले P तथा Q का व्यास क्रमशः 1 सेमी एवं 0.5 सेमी है। गोले P को 0.8 ग्राम/सेमी3 घनत्व एवं η=3 प्वॉइजली श्यानत्व वाले एक तरल में गिराया जाता है और गोले Q को 1.6 ग्राम/सेमी3 घनत्व एवं η=2 प्वॉइजली श्यानत्व वाले दूसरे तरल में गिराया जाता है। गोले P एवं Q के अन्तिम वेगो का अनुपात क्या होगा?
01:48View SolutionThe external and internal diameters of a hollow sphere are 6 cm and 8 cm respectively. The sphere floats completely immersed in a liquid of density 1.2g⋅cm−3. What is the density of the material of the sphere?
07:12View SolutionIf the terminal speed of a sphere of gold (density =19.5kgm−3) density of liquid =1.5kgm−3) is 0.2ms−1 in a viscous liquid . What is the terminal speed of a sphere of silver (density =10.5kgm−3) of the same size in the same liquid ?
04:22View SolutionThe critical velocity of the flow of a liquid through a pipe of radius 3 is given by vc=(Kηrp), where p is the density and η, is the coefficient of viscosity of liquid. Check if this relation is dimentionally correct.
03:33View Solution

