A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
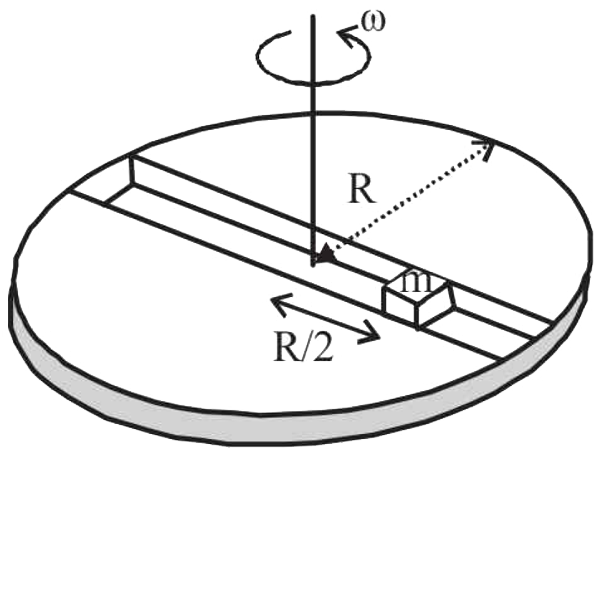
The distance r of the block at time is
R4(eωt+e−ωt)
R2cosωt
R4(eωt+e−ωt)
R2cosωt
Step by step video & image solution for A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega. where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk). A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Part I : PHYSICS (Section 2)
13 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Part I : PHYSICS (Section 3)Paragraph 2
2 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION 1)
13 Videos
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
Similar Questions
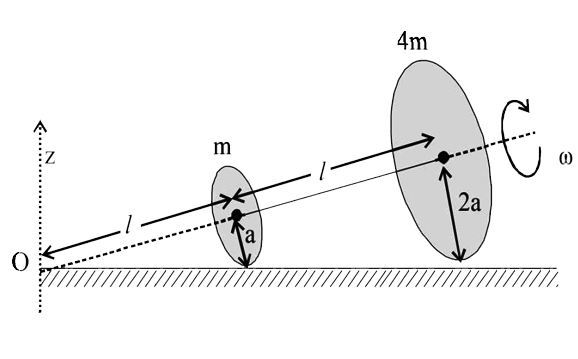
Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length l=√24a through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momemtum of the entire assembly about the point 'O' is vacL (see the figure). Which of the follwing statement (s) is (are) true?
View SolutionOne twirls a circular ring (of mass and radius ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is ?. The finger rotates with an angular velocity 20. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is μ and the acceleration due to gravity is g.
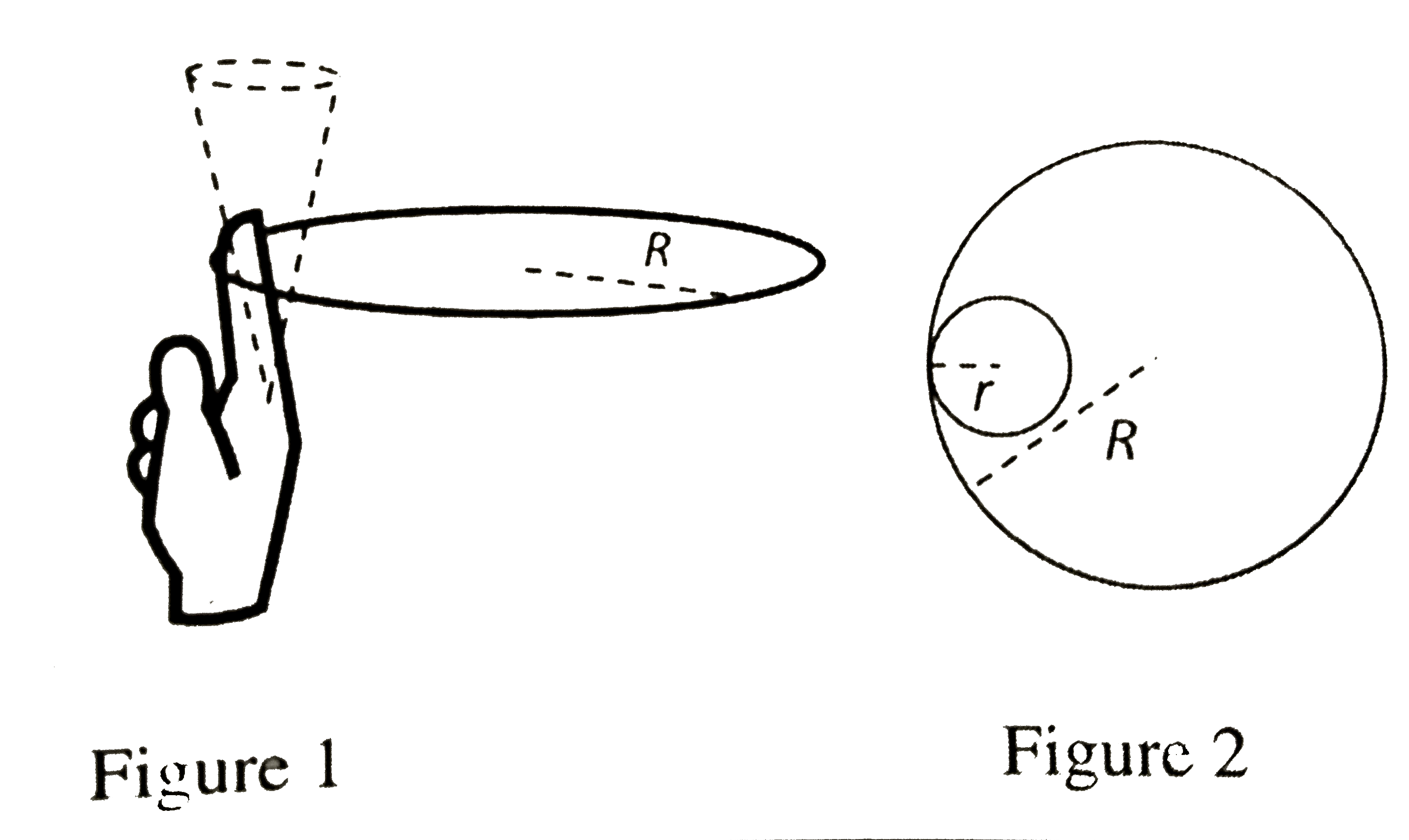
The minimum vlaue of ω0 below which the ring will drop down is
View SolutionThe electrostatic energy of Z protons uniformly distributed throughout a spherical nucleus of radius R is given by
E=3Z(Z−1)e25(4πe0R)
The measured masses of the neutron _(1)1H,157Nand,168Oare1.008665u,1.007825u,15.000109uand15.003065u, respectively Given that the ratio of both the _(7)12N and _(8)15O nucleus are same , 1 u = = 931.5 Me Vc2 (c is the speed of light ) and e2/(4πe0)=1.44MeV fm Assuming that the difference between the binding energies of _715Nand_(8)^(15) O is purely due to the electric energy , The radius of the nucleus of the nuclei is
View SolutionA spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
View SolutionPut a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
View SolutionNON-INERTIAL FRAME OF REFERENCE
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The net reaction of the disc on the block is
View SolutionAssertion : A reference frame attached to earth is an inertial frame of reference.
Reason : The reference frame which has zero acceleration is called a non inertial frame of reference.
View SolutionIn an inertial frame of reference, the magnetic force on a moving charged particle is F. Its value in another inertial frame of reference will be
View SolutionDistinguish between inertial and non-inertial frames of reference.
View SolutionDefine inertial and non-inertial frames of reference with example.
View SolutionDefine inertial frame and non-inertial frame. Is earth an inertial frame of reference?
View Solution(A) : A reference frame attached to earth is a non inertial frame of reference.
(R) : The reference frame which has an acceleration is called a non inertial frame of reference.
View SolutionIn an inertial frame of reference, the magnetic force on a moving charged particle is F. Its value in another inertial frame of reference will be
View SolutionExplain inertial frame of reference and non- inertial frame of reference.
View Solution
