Three vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
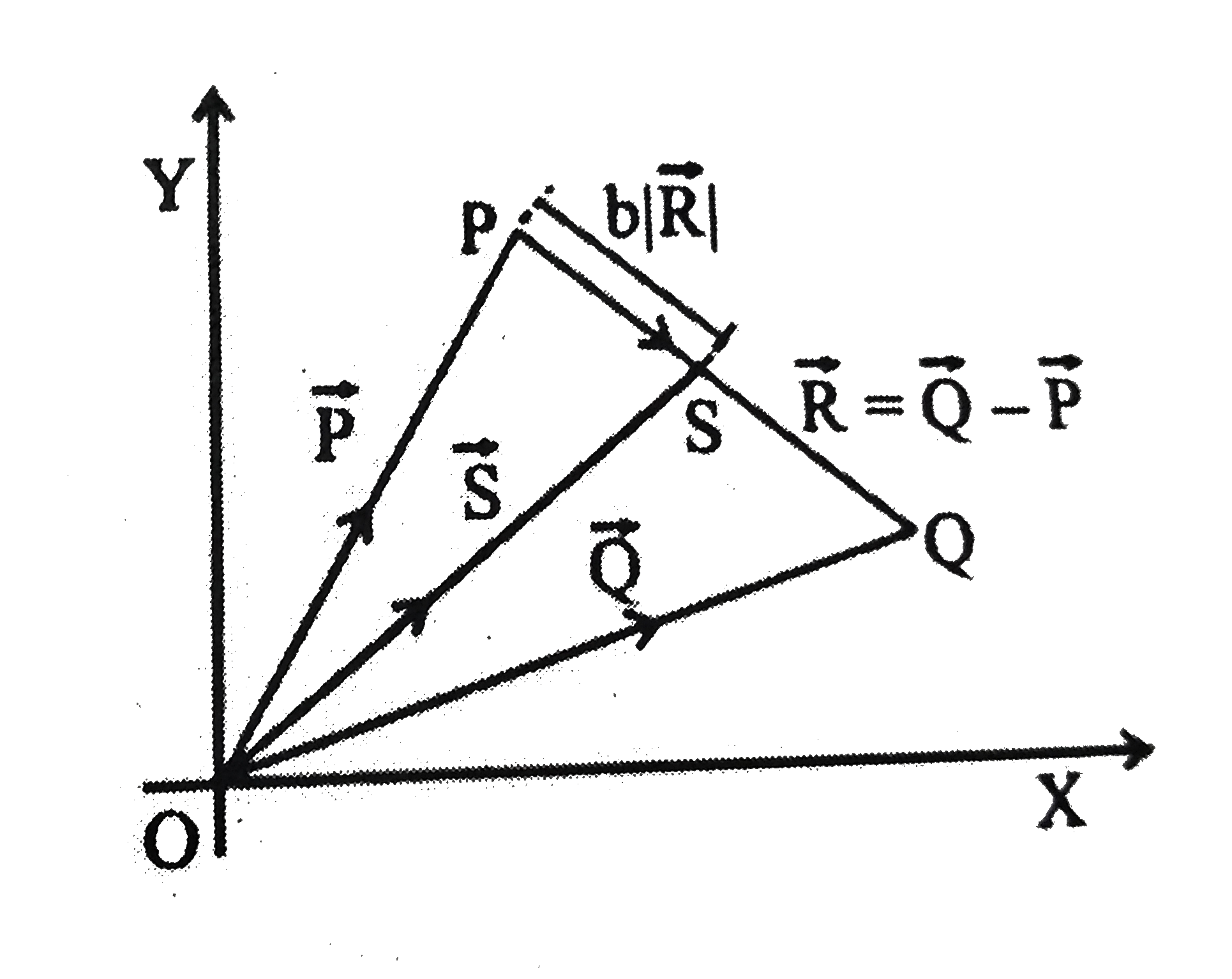
→S=(1−b)→P+b→Q
→S=(b−1)→P+b→Q
→S=(1−b2)→P+b→Q
→S=(1−b)→P+b2→Q
The correct Answer is:A
Step by step video & image solution for Three vectors vecP,vecQ " and " vecR are shown in the figure. Let S be any point on the vector vecR. The distance between the points P and S is b|vecR|. The general relation among vectors vecP,vecQ " and " vecS is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Three vectors ¯¯¯P,¯¯¯Qand¯¯¯R are shown in the figure.Let S be any point on the vector bar(R) .The distance between the points P and S is b|bar(R)| .The general relation among vectors bar(P) bar(Q) and bar(S) is qquad Y
View SolutionThree vectors bar(P) bar(Q) and bar(R) are shown in the figure.Let S be any point on the vector bar(R) .The distance between the points P and S is b|bar(R)| .The general relation among vectors bar(P) bar(Q) and bar(s) is
View Solution
Knowledge Check
If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
Acos−1(512)Bcos−1(513)Ccos−1(1213)Dcos−1(213)If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
Acos−1(512)Bcos−1(513)Ccos−1(1213)Dcos−1(213)If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
ACos−1(512)BCos−1(513)CCos−1(1213)DCos−1(213)
The vectors →Pand→Q have equal magnitudes of →P+→Q is n times the magnitude of →P−→Q, then angle between →P and →Q is:
View SolutionThere are three forces →P,→Qand→R are acting on a body in the x y-plane, the angle between →Pand →Q and →Q and →R are 150∘and120∘ respectively. Find the value of a + b + c,if →P:→Q:→R
is equal to √a : b : c, for system is in equilibrium?
View SolutionFor three vectors →P,→Qand→R,→P+→Q=→RandP+Q=R
Then prove that →Pand→Q are parallel to each other.
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P∣∣−∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View Solutionif ∣∣→P+→Q∣∣=∣∣→P∣∣+∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View Solution
