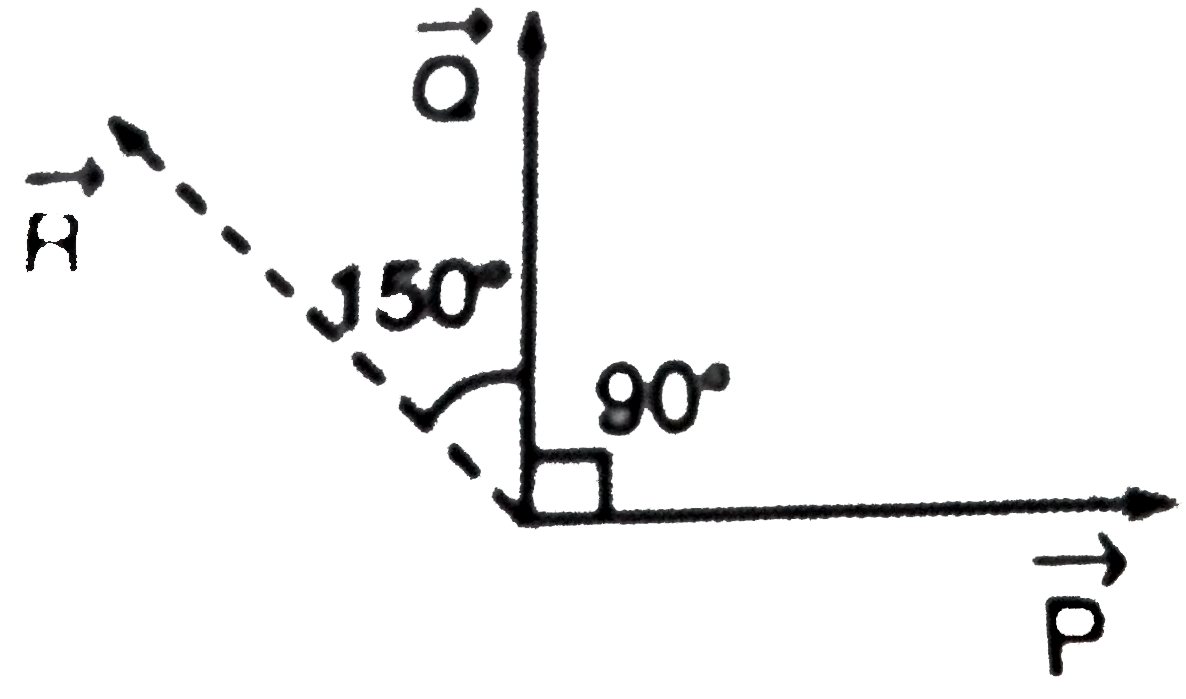
Three vectors $\to P, \to Q$ and $\to R$ such that $∣ ∣ \to Q ∣ ∣ = A \sqrt{2}$ and the angles between $\to P$ and $\to Q, \to Q$ and $\to R, \to R$ and $\to P$ are $90^{\circ}, 150^{\circ}, 120^{\circ}$ respectivlely. Find the value of $∣ ∣ \to P ∣ ∣ =$

$\frac{A}{\sqrt{2}}$

$\frac{A \sqrt{2}}{\sqrt{3}}$

$\frac{2 A}{\sqrt{3}}$

$\frac{A}{2}$

Text Solution

Verified by Experts

The correct Answer is:b

Updated on:21/07/2023

If $\to P . \to Q = P Q$ then angle between $\to P$ and $\to Q$ is
A $0^{\circ}$
B $30^{\circ}$
C $45^{\circ}$
D $60^{\circ}$
If $∣ ∣ \to P + \to Q ∣ ∣ = ∣ ∣ \to P - \to Q ∣ ∣$ the angle between $\to P and \to Q$ is
A $0^{\circ}$
B $90^{\circ}$
C $180^{\circ}$
D $45^{\circ}$
What is the angle between $\to P$ and the resultant of $(\to P + \to Q)$ and $(\to P - \to Q)$
AZero
B ${tan}^{- 1} (P / Q)$
C ${tan}^{- 1} (Q / P)$
D ${tan}^{- 1} (P - Q) / (P + Q)$