One twirls a circular ring (of mass and radius ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is ?. The finger rotates with an angular velocity 20. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is μ and the acceleration due to gravity is g.
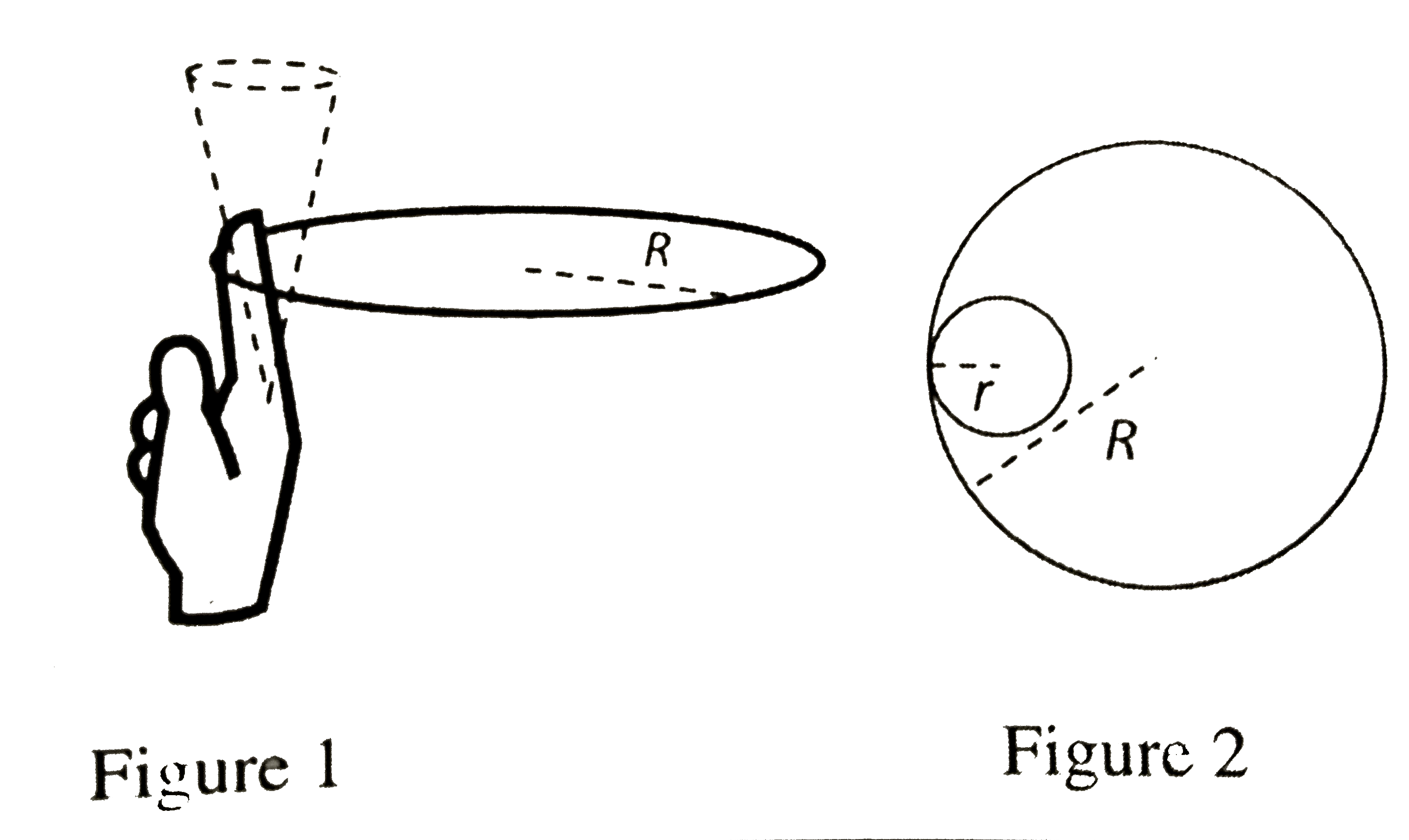
The minimum vlaue of ω0 below which the ring will drop down is
M2s0R2
12M23c(X1)2
Mω++20(R−τ)s
32Mω20(R−r)2
The correct Answer is:A, B, C, D
Step by step video & image solution for One twirls a circular ring (of mass and radius ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is ?. The finger rotates with an angular velocity 2_(0). The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is mu and the acceleration due to gravity is g. The minimum vlaue of omega_(0) below which the ring will drop down is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION 16videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION 27videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Part I : PHYSICS (Section 2)13videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 36videos
JEE (ADVANCE) 2020
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-36videos
JEE ADVANCED 2020
Similar Questions
The potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
03:45View SolutionTwo men are walking along a horizontal straight line in the same direction. The man in front walks at a speed 1.0 ms−1 and the man behind walks at a speed 2.0ms−1. A third mad is standing at a height 12m above the same horizontal line such that all three men are in a vertical plane. The two walking men are blowing identical whistles which emit a sound of frequency 1430 Hz. The speed of sound in air is 330 ms−1. At the instant, when the moving men are 10 m apart, the stationary man is equidistant from them. The frequency of beats in Hz, heard by the stationary man at this instant, is
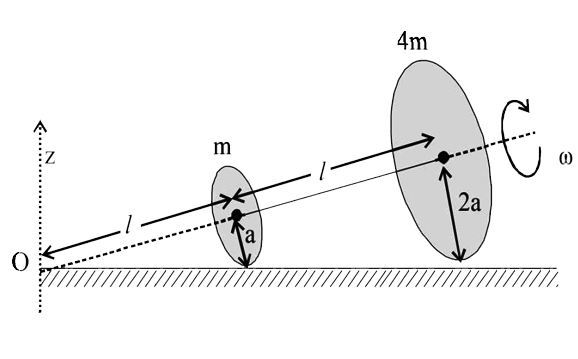
01:09View SolutionTwo thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length l=√24a through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momemtum of the entire assembly about the point 'O' is vacL (see the figure). Which of the follwing statement (s) is (are) true?
 01:09View Solution
01:09View SolutionA spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
04:50View SolutionPut a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
01:49View SolutionOne twirls a circular ring (of mass and radius ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is ?. The finger rotates with an angular velocity 20. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is μ and the acceleration due to gravity is g.

The minimum vlaue of ω0 below which the ring will drop down isView SolutionIn how many ways five different rings can be worn in four fingers with at least one ring in each finger?
05:21View SolutionIn how many ways five different rings can be put on four fingers with at least one ring on each finger?
06:58View Solutionयदि अंगूठे के लिए एक, तर्जनी (Index ) उँगली के लिए दो, मध्यमा (Middle) के लिए तीन, अनामिका (Ring) उँगली के लिए चार, कनिष्ठिका (Little) उँगली के लिए पाँच और इसी प्रकार पीछे से गणना करते हुए छह अनामिका उँगली के लिए सात मध्यमा उँगली के लिए, आठ तर्जनी उँगली के लिए, नौ अंगूठे के लिए, दस तर्जनी उँगली के लिए, ग्यारह मध्यमा उँगली के लिए, बारह अनामिका उँगली के लिए, तेरह कनिष्ठिका उँगली के लिए, चौदह अनामिका उँगली और इसी तरह आगे भी गिनती करते जाएँ तो किस उँगली के लिए एक हज़ार गिनेगें।
01:05View SolutionThere are 7 distinguishable rings. The number of possible five - rings arrangements on the four fingers (except the thumb) of one hand (the order of the rings on each finger is to be counted and it is not required that each finger has a ring is equal to
05:11View SolutionGiven eight distinguishable rings, the number of possible five ring arrangements on the four fingers (not the thumb) of one hand is (the order of the rings on each finger is significant, but it not required that such that each finger have a ring) is
06:58View Solutionएक वृत्ताकार वलय (circular ring)(द्रव्यमान M एवं त्रिज्या R) एक उंगली के परित ध्रुतघूर्णन करता है (जैसा चित्र 1 (figure 1) में दर्शाया गया है) इस प्रक्रम में उंगली वलय के अंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु (cone) के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे कि बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श विन्दु के अनुरेखिय पथ की त्रिज्या r है। उंगली कोणीय वेग ω0 से घूर्णन कर रही है। वलय r त्रिज्यावाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन (rolls without slipping) करता है। जैसा चित्र 2 (figure2) में वलय एवं उंगली के स्पर्श बिंदु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक (coefficient of friction) μ एवं गुरूत्वीय त्वरण g है।
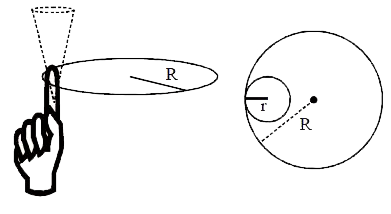
वलय की कुल गतिज ऊर्जा है05:21View Solutionएक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर्णन करता है (जैसा चित्र 1 में दर्शाया गया है)। इस प्रक्रम में उंगली वलय के आंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे की बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श बिन्दु के अनुरेखिय पथ की त्रिज्या । है। उंगली कोणीय वेग ω0 से घूर्णन कर रही है। वलय । त्रिज्या वाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन करता है। जैसा चित्र 2 में वलय एवं उंगली के स्पर्श बिन्दु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक μ एवं गुरूत्वीय त्वरण g है
न्यूनतम ω0 जिसके कम होते ही वलय गिर जायेगा वह है01:24View SolutionIdentify and write the common property" of the following collections.
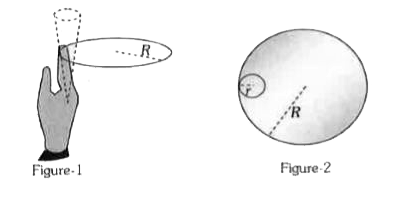
Thumb,index finger, middle finger, ring finger, little finger02:03View Solutionएक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर्णन करता है (जैसा चित्र 1 में दर्शाया गया है)। इस प्रक्रम में उंगली वलय के आंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे की बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श बिन्दु के अनुरेखिय पथ की त्रिज्या । है। उंगली कोणीय वेग ω0 से घूर्णन कर रही है। वलय । त्रिज्या वाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन करता है। जैसा चित्र 2 में वलय एवं उंगली के स्पर्श बिन्दु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक μ एवं गुरूत्वीय त्वरण g है

वलय की कुल गतिज ऊर्जा02:15View Solutionएक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर्णन करता है (जैसा चित्र 1 में दर्शाया गया है)। इस प्रक्रम में उंगली वलय के आंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे की बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श बिन्दु के अनुरेखिय पथ की त्रिज्या । है। उंगली कोणीय वेग ω0 से घूर्णन कर रही है। वलय । त्रिज्या वाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन करता है। जैसा चित्र 2 में वलय एवं उंगली के स्पर्श बिन्दु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक μ एवं गुरूत्वीय त्वरण g है

न्यूनतम ω0 जिसके कम होते ही वलय गिर जायेगा वह है03:43View Solution

