Divide 5x3−13x2+21x−14 by (3−2x+x2) and verify the division algorithm.
First we write the given polynomials in standard form in decreasing order of degrees and then perform the division as shown below.
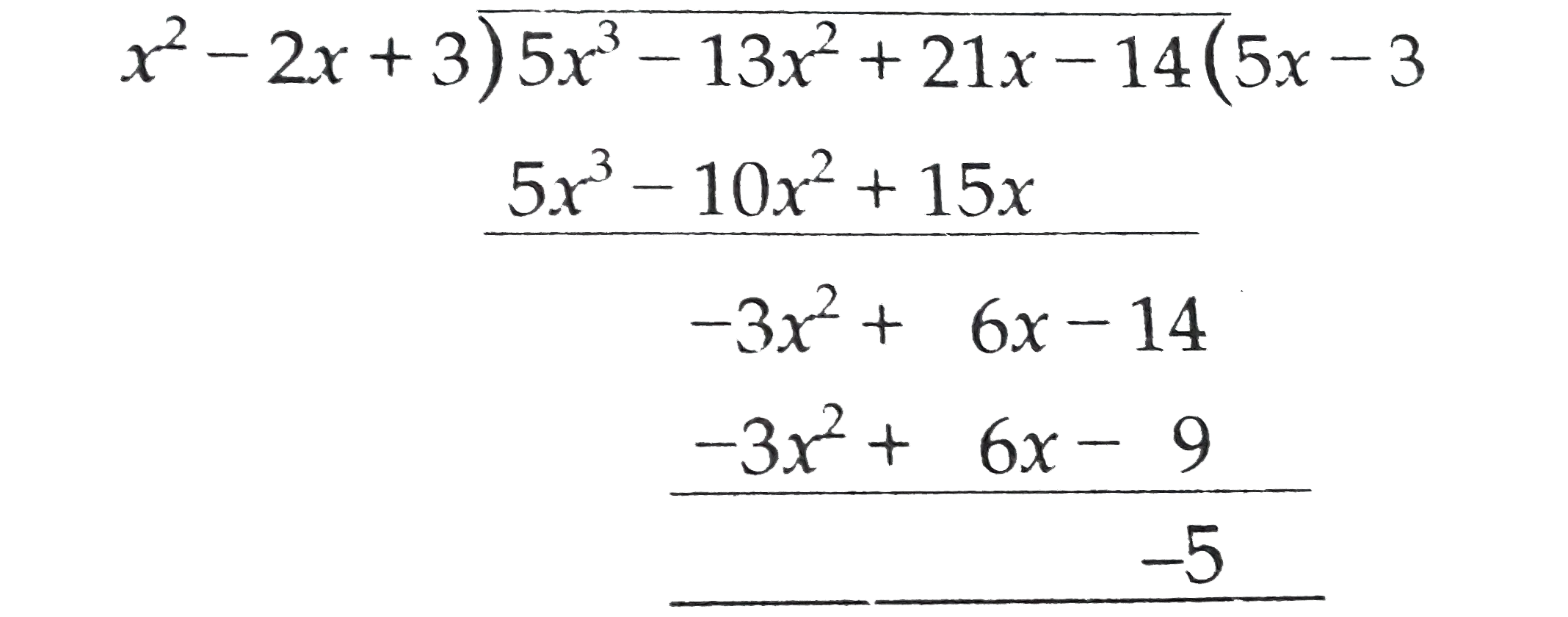
Clearly, degree (−5)=0< degree (x2−2x+3).
∴ quotient = (5x-3) and remainder =- 5
⇒ (quotient × divisor) + remainder
=(5x−3)(x2−2x+3)−5
5x3−10x2+15x−3x2+6x−9−5
=5x(3)−13x2+21x−14
= dividend.
Thus, (quotient × divisor)+ remainder = dividend.
Hence, the division algorithm is verified.
Topper's Solved these Questions
- POLYNOMIALSBook:RS AGGARWALChapter:POLYNOMIALSExercise:Exercise 2A
Explore 21 Videos
- POLYNOMIALSBook:RS AGGARWALChapter:POLYNOMIALSExercise:Exercise 2B
Explore 19 Videos
- PERIMETER AND AREA OF PLANE FIGURES Book:RS AGGARWALChapter:PERIMETER AND AREA OF PLANE FIGURES Exercise:TEST YOURSELF (SHORT -ANSWER QUESTIONS)
Explore 1 Video
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 37 Videos
Similar Questions
Divide 4x2−11x2+7x−2 by 1+x−x2 and verify the division algorithm.
Note
Always write the divided and divisor in standard form i.e., decreasing order of the variable.
View SolutionDivide 2x4−9x3+5x2+3x−8 by x2−4x+1 and verify the division by algorithm.
View SolutionDivide 3−x+2x2 by (2-x) and verify the division algorithm.
View SolutionDivide 2x2+4x3+5x−6 by 2x2+1+3x and verify the division algorithm
View SolutionDivide 2x2+x−5 by x+2 and verify the division algorithm.
View SolutionDivide x -4x3 8x2 t 7x 10 by (x 2) and verify the division algorithm.
View SolutionDivide x4+5x3−x2+4x−3 by x-2 and verify the division algorithm.
View SolutionDivide 3x2−x3−3x+5by x−1−x2, and verify the division algorithm.
View SolutionDivide : (x2−4x+3) by ( x - 1 ) and verify the division algorithm.
View SolutionDivide the polynomical 6x4−44x2+6x−3 by the polynomial x2−3x+ 1 and verify the division algorithm.
View Solution