Find the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers. Solution in Telugu
The correct Answer is:(i) -2 (ii) 2 (iii) −32(iv)32 (v) 0 (vi) 0 (vii) (-q)/(p)
Step by step video, text & image solution for Find the zero of the polynomial in each of the following cases. (i) f (x) = x +2 (ii) f (x) = x-2 (iii) f (x) =2x +3 (iv) f (x) =2x -3 (v) f (x) =x ^(2) (vi) f (x) = px, p ne 0 (vii) f (x) = px + q,p ne 0 pq are real numbers. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NCERT TELUGUCHAPTER - POLYNOMIALS AND FACTORISATION EXERCISE - EXERCISE 2.39videos
POLYNOMIALS AND FACTORISATION
- BOOK - NCERT TELUGUCHAPTER - POLYNOMIALS AND FACTORISATION EXERCISE - EXERCISE 2.49videos
POLYNOMIALS AND FACTORISATION
- BOOK - NCERT TELUGUCHAPTER - POLYNOMIALS AND FACTORISATION EXERCISE - EXERCISE 2.16videos
POLYNOMIALS AND FACTORISATION
- BOOK - NCERT TELUGUCHAPTER - LINES AND ANGLES EXERCISE - THINK, DISCUSS AND WRITE3videos
LINES AND ANGLES
- BOOK - NCERT TELUGUCHAPTER - PROBABILITY EXERCISE - EXERCISE 14.121videos
PROBABILITY
Similar Questions
Find the remainder when x3+3x2+3x+1 is divided by the following Linear polynomials:
(i) x+1
(ii) x−12
(iii) x
(iv) x+π
(v) 5+2x04:07View SolutionDetermine which of the following polynomials has (x+1) as a factor.
(i) x3−x2−x+1
(ii) x4−x3+x2−x+1
(iii) x4+2x3+2x2+x+1
(iv) x3−x2−(3−√3)x+√3View SolutionFind the degree of each of the polynomials given below
(i)x5−x4+3
(ii) x2+x−5
(iii) 5
(iv) 3x6+6y3−7
(v) 4−y2
(vi) 5t−√303:37View SolutionWhat is the difference between intersecting lines and concurrent lines ?
02:12View SolutionA die has six faces numbered from 1 to 6. It is rolled and the number on the top face is noted. When this is treated as a random trial.
What are the possible outcomes ?01:35View SolutionLet f(x) be a polynomial with real coefficients such that f(0)=1 and for all x ,f(x)f(2x^(2))=f(2x^(3)+x) The number of real roots of f(x) is:
03:07View SolutionThe graph of y = f(x) is as shown in the following figure.
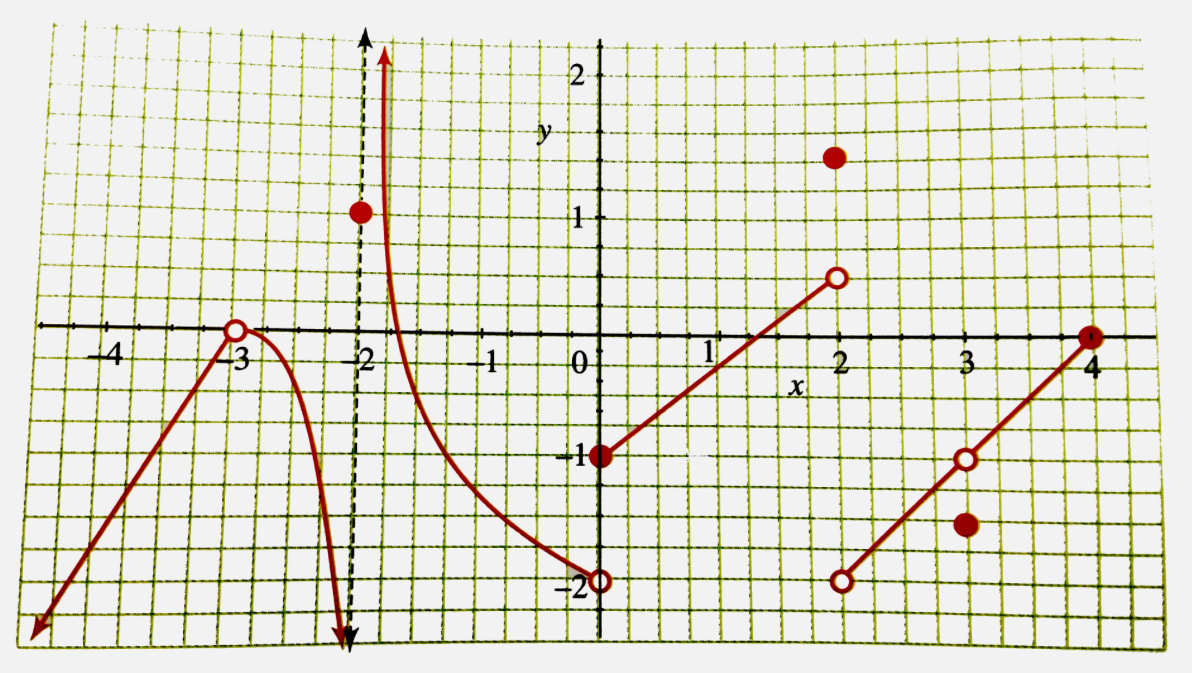
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)03:02View SolutionIf f(x)=x3−2px2−4x+5 and f'(2)=0 find p .
02:18View SolutionThe weakest acid HX ( X = F , Cl ,Br, I) is _________.
View SolutionLet f(x) = 2x + 5. If x ≠ 0 then find
f(x+2)−f(2)x09:39View SolutionThe order of reactivity of halogens is
(A) F>Cl>Br>I
(B) F < Cl < Br < I
(C) F < Cl > Br < I
(D) F < Cl < Br> I03:14View SolutionFind the zeros of the polynomial in each of the following.
(i) p(x)=x−3
(ii) p(x)=2x+5
(iii) q(y)=2y−3
(iv) f(z)=8z
( v) p(x)=axwhen a ≠ 0
(vi) h( x) =ax + b , a ne 0, a, b in R07:55View SolutionFind the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers.02:01View SolutionFind the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers.00:51View SolutionFind the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers.06:19View Solution

