Obtain equations of motion for constant acceleration using method of calculus.Solution in Bengali
By definition
a=dυdt
dυ=adt
Integrating both sides
∫υυ0dυ=∫t0adt
=a∫t0dt (a is constant)
υ−υ0=at
υ=υ0+at
Further, υ=dxdt
dx=υdt
Integrating both sides
∫xx0dx=∫t0υdt
=∫t0(υ0+at)dt
x−x0=υ0t+12at2
x=x0+υ0t+12at2
We can write
a=dυdt=dυdxdxdt=υdυdx
or υdυ=adx
Integrating both sides,
∫υυ0υdυ=∫xx0adx
υ2−υ202=a(x−x0)
υ2=υ20+2a(x−x0)
The advantage of this method is that it can be used for motion with non-uniform acceleration also. Now, we shall use these equations to some important cases. t
Topper's Solved these Questions
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISES21videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES5videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A PLANEEXERCISE - EXCERCISES30videos
MOTION IN A PLANE
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
Similar Questions
In which of the following examples of motion, can the body be considered approximately a point object:
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.08:38View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
03:58View SolutionState , for each of the following physical quantities , if it is a scalar or a vector : volume , mass , speed , acceleration , density , number of moles , velocity , angular frequency , displacement , angular velocity .
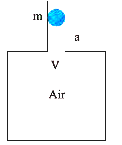
07:17View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 07:17View Solution
07:17View SolutionDerivations Of Equation Of Motion By Calculus Method
10:53View SolutionDeduce the equations of unifromly accelerated motion in one dimension by following calculus method.
56:44View SolutionDerive equations of uniformly acceleration motion by calculus method.
10:42View SolutionDerive equations of uniformly acceleration motion by calculus method.
04:43View SolutionObtain equations of motion for constant a acceleration using the method of calculus.
05:48View SolutionMotion With Constant Acceleration|Equation Of Motion
03:26View SolutionDerive the equations of motion for an object in uniformly accelerated motion in one dimension using calculus.
07:13View SolutionObtain equations of motion for constant acceleration using method of calculus.
04:46View SolutionObtain equations of motion for constant acceleration using method of calculus.
05:21View SolutionDerive the equations of uniformaly accelerated motion by graphical method.
07:25View SolutionObtain equations of motion for constant acceleration using method of calculus.
04:43View Solution

