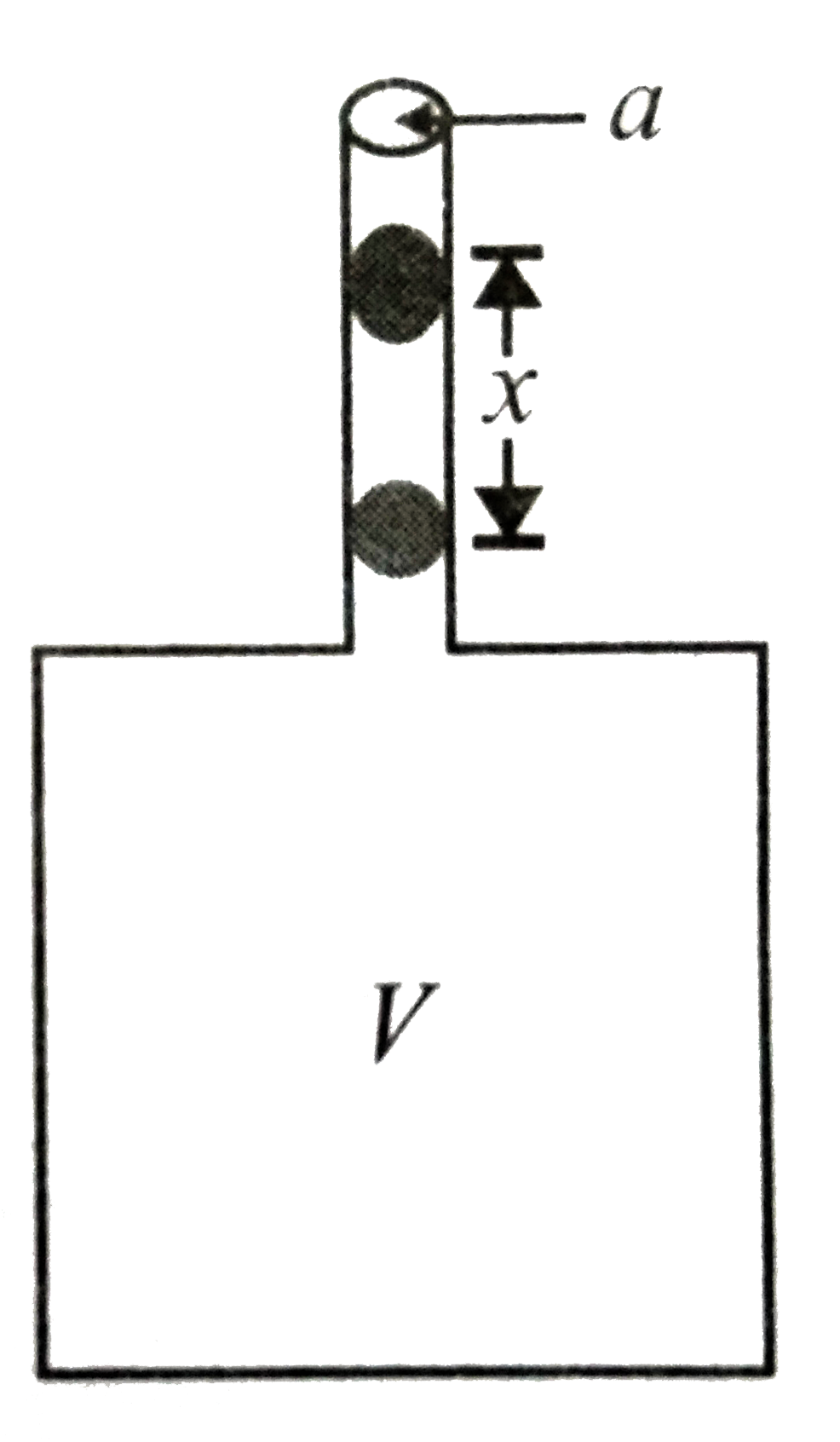
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
![An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BEN_PHY_XI_P2_C14_E01_029_Q01.png)
where B is the bulk modulus of air. For isothermal changes B=P.
Topper's Solved these Questions
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercises27videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES5videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)3videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time periodof oscillations assuming pressure volume variatinos of air to be isothermal.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solution
Knowledge Check
- Question 1 - Select One
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
AT=2π√Ba2mVBT=2π√BVma2CT=2π√mBVa2DT=2π√mVBa2 - Question 2 - Select One
An air chamber of volume V has a neck of cross-sectional area a into which a light ball of mass m just fits and can move up and down without friction. Consider diameter of the ball to be equal to that of the neck of the chamber. The ball is then pressed down a little and released. Let the bulk modulus of air is B. The time period of the oscillation of the ball is:
AT=2π√Ba2mVBT=2π√BVma2CT=2π√mBVa2DT=2π√mVBa2 - Question 3 - Select One
An air chamber of volume V has a long of cross sectional area A. A ball of mass m is fixed sympthlly in the track The ball modulus of air is B ball is pressed down slightly and released, the time period of the oscillation is
A2π√mV2BA2Bπ√2mVBA2C2π√mVBA2Dπ2√mBA2
An air chamber of volume v has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released for the time priod of oscillation, assuming pressure-volume variations of the air to be isothermal.
View SolutionAn air chamber of volume V has a neck of crosssectional area "a' into which a light ball of mass "m' just fits and can move up and down without friction. The diameter of the ball is equal to that of the neck of the chamber. The ball is pressed down a little and released. If the bulk modulus of air is B the time period of the oscillation of the ball is 2πmxVyBza9. The value of xyq is
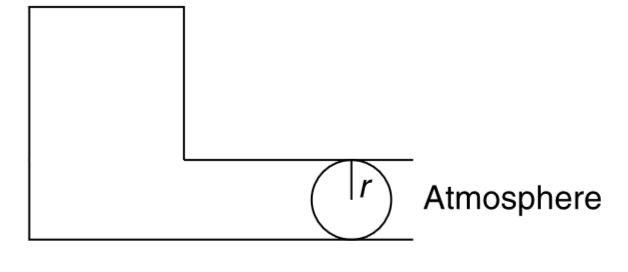
View SolutionA ball of radius r fits tightly inside a tube attached to a container. There is no friction between the tube wall and the ball. Volume of air inside the container is V0 when the ball is in equilibrium. Density of the material of the ball is d and atmospheric pressure is P0. If the ball is displaced a little from its equilibrium position and released, find time period of its oscillation. Assume that temperature in the container remains constant and that air is an ideal gas.
View SolutionA rectangular pipe having cross sectional area A. It is closed at one end and at its other end ablock having same cross-section and mass 'm' is placed such that system is air tight. Inequilibrium position of block the pressure and volume of air enclosed in pipe are P and Vrespectively. If block is displaced by small distance x inward and released then find the timeperiod of S.H.M. [Assume the walls are frictionless and compression of air is isothermal].
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
The time period of oscillation for small displacements of the piston isView Solution