Stopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (υ0) and the braking capacity, or deceleration, −a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of υ0 and a.Solution in Bengali
Let the distance travelled by the vehicle before it stops be ds. Then, using equation of motion υ2=υ20+2ax, and noting that υ=0, we have the stopping distance
ds=−υ202a
Thus, the stopping distance is proportional to the square of the initial velocity. Doubling the initial velocity increases the stopping distance by a factor of 4 (for the same deceleration). For the car of a particular make, the braking distance was found to be 10 m, 20 m, 34 m and 50 m corresponding to velocities of 11, 15, 20 and 25 m/s which are nearly consistent with the above formula. Stopping distance is an important factor considered in setting speed limits, for example, in school zones.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISES
21 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- MOTION IN A PLANEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A PLANEEXERCISE - EXCERCISES
30 Videos
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
Similar Questions
In which of the following examples of motion, can the body be considered approximately a point object:
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
View SolutionState , for each of the following physical quantities , if it is a scalar or a vector : volume , mass , speed , acceleration , density , number of moles , velocity , angular frequency , displacement , angular velocity .
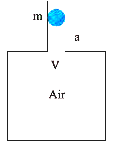
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initialy velocity (v_(0)) and the braking capacity, or deceleration -a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of v_(0) and a .
View Solutionवाहनों की अवरोधन दूर : अवरोधन दुरी से हमारा अभिप्राय उस दुरी से है जो गतिमान वस्तु ब्रेक लगाने के कारण रूकने से पहले चल चुकी होती है | सड़क पर गतिमान वाहनों की सुरक्षा के संबंध में यह एक महत्वपूर्ण कारक है | यह दुरी वाहन के प्रारंभिक वेग (v0) तथा उसके ब्रेक की क्षमता या ब्रेक लगाए जाने के परिणामस्वरूप वाहन में उत्पन्न मंदन -a पर निर्भर करती है | किसी वाहन की अवरोधन दुरी के लिएv0 तथा a के पदों में व्यंजक निकालिए |
View Solutionएक मोटर गाडी द्वारा ब्रेक लगाने के बाद t सेकण्ड में तय की दूरी s फ़ीट है जहां s=22t−12t2 मोटर रुकने के पहले तक तय की दूरी निकालें |
View Solutionब्रेक लगाने से एक चलती हुई गाड़ी रुक जाती है। इस प्रक्रिया में गाड़ी के संवेग का क्या होता है?
View Solutionवाहनों की अवरोधन दूरी : अवरोधन दूरी से हमारा अभिप्राय उस दूरी से है जो गतिमान वस्तु ब्रेक लगाने के कारण रुकने से पहले चल चुकी होती है | सड़क पर गतिमान वाहनों की सुरक्षा के सम्बन्ध में यह एक महत्त्वपूर्ण कारक है | यह दूरी वाहन के प्रारम्भिक वेग (v0) तथा उसके ब्रेक की क्षमता या ब्रेक लगाए जाने के परिणामस्वरूप वाहन में उत्पन्न मंदन - a पर निर्भर करती है | किसी वाहन की अवरोधन दूरी के लिए v0 तथा a के पदों में व्यंजक निकालिए |
View SolutionGet an expression for stopping distance of a vehicle in terms of intial velocity va and deceleration "a"…
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (υ0) and the braking capacity, or deceleration, −a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of υ0 and a.
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (υ0) and the braking capacity, or deceleration, −a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of υ0 and a.
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (upsilon_(0)) and the braking capacity, or deceleration, -a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of upsilon_(0) and a.
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initialy velocity (v_(0)) and the braking capacity, or deceleration -a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of v_(0) and a .
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (υ0) and the braking capacity, or deceleration, −a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of υ0 and a.
View Solution
