Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
The correct Answer is:2.8×10−6
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDS BOOK - NCERT BANGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDS EXERCISE - Exercises
16 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - NCERT BANGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE
43 Videos
- MOTION IN A PLANEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A PLANEEXERCISE - EXCERCISES
30 Videos
Similar Questions
Four identical hollow cylindrical cloumns of steel support a big structure of mass 50.000 kg. the inner and outer radii of each column are 30 cm and 60 cm respectively. Assume the load distribution to be uniform , calculate the compressional strain of each column. the Young's modulus of steel is 2.0×1011Pa.
View SolutionFour identical hollow cylindrical columns, support a ig structure of mass M. The inner and outer radii of a column are R1, and R2, respectively. Assuming the load distribution to be uniform, the compressional strain of each column is
(where Y is Young's modulus of the column).
View Solution
Knowledge Check
Four identical hollow cylindrical cloumns of steel support a big structure of mass 50.000 kg. the inner and outer radii of each column are 30 cm and 60 cm respectively. Assume the load distribution to be uniform , calculate the compressional strain of each column. the Young's modulus of steel is 2.0×1011Pa.
AMgπ(R22−R21)YBMg4π(R22−R21)YCMgπ(R21−R22)YDMg4π(R21−R22)YA hollow cylindrical column of steel supports a load of 20,000 kg. The inner and the outer radii of the column are 50 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of the column. Given, Young's modulus of steel =2.0×1011Nm2 and g=10ms−2.
A7×10−16B2.895×10−10C5.8×10−12D2.895×10−6
Four identical hollow cylindrical columns of mild steel support a big structure of mass 50×103kg .The inner and outer radii of each column are are 50 cm and 100 cm respectively. Assuming uniform local distribution ,calculate the compression strain of each column. [use Y=2.0×1011Pa,g=9.8m/s2]
View SolutionA hollow cylindrical column of steel with inner and outer radii 20cm and 30cm supports a load of 12,000 kg. Assume the load distribution to be uniform. The value of compressional strain in terms of 10- 6 of the column is ... (Take Ysteel=2×1011Pa,π = 3. 14, g = 9. 8 m/s2
View SolutionIn the system shown in the figure blocks A and B have mass m1=2kg and m2=26/7kg respectiely. Pulley having moment of inertia I=0.11kgm−2 can rotate without friction about a fixed axis. Inner and outer radii of pulley are a=10cm and b=15cm respectively. B is hanging with the thread wrapped around the pulley, while A lies on a rough inclined plane.
Coefficient of friction being μ=√3/10
Calculate
as. Tension in each thread, and
b. Acceleration of each block (g=10ms−2)

View SolutionIn the system shown in the figure blocks A and B have mass m1=2kg and m2=26/7kg respectively. Pulley having moment of inertia I=0.11kgm−2 can rotate without friction about a fixed axis. Inner and outer radii of pulley are a=10cm and b=15cm respectively. B is hanging with the thread wrapped around the pulley, while A lies on a rough inclined plane.
Coefficient of friction being μ=√3/10
Calculate
as. Tension in each thread, and
b. Acceleration of each block (g=10ms−2)

View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
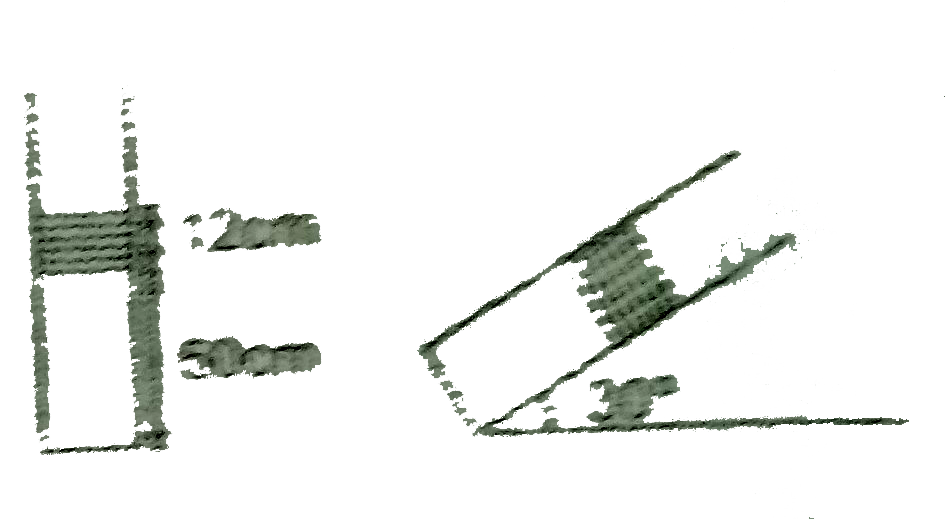
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)

View Solution
