In the system shown in the figure blocks A and B have mass m1=2kg and m2=26/7kg respectively. Pulley having moment of inertia I=0.11kgm−2 can rotate without friction about a fixed axis. Inner and outer radii of pulley are a=10cm and b=15cm respectively. B is hanging with the thread wrapped around the pulley, while A lies on a rough inclined plane.
Coefficient of friction being μ=√3/10
Calculate
as. Tension in each thread, and
b. Acceleration of each block (g=10ms−2)

When the system is released, weight m2g tries to rotate the pulley in clockwise direction while down the plane component m1gsin30∘ of weight of block A tries to rotate it anticlockwise but moment produced by m2g is greater, therefore, the pulley has tendency to rotated clockwise. Let is angular acceleration be αr. The acceleration of blocks A and B will be equal to aα(up the plane) and bα (vertically downwards) respectively.
Let tension in threads connected with blocks A and B be T1 and T2, respectively.
Considering free body diagrams .
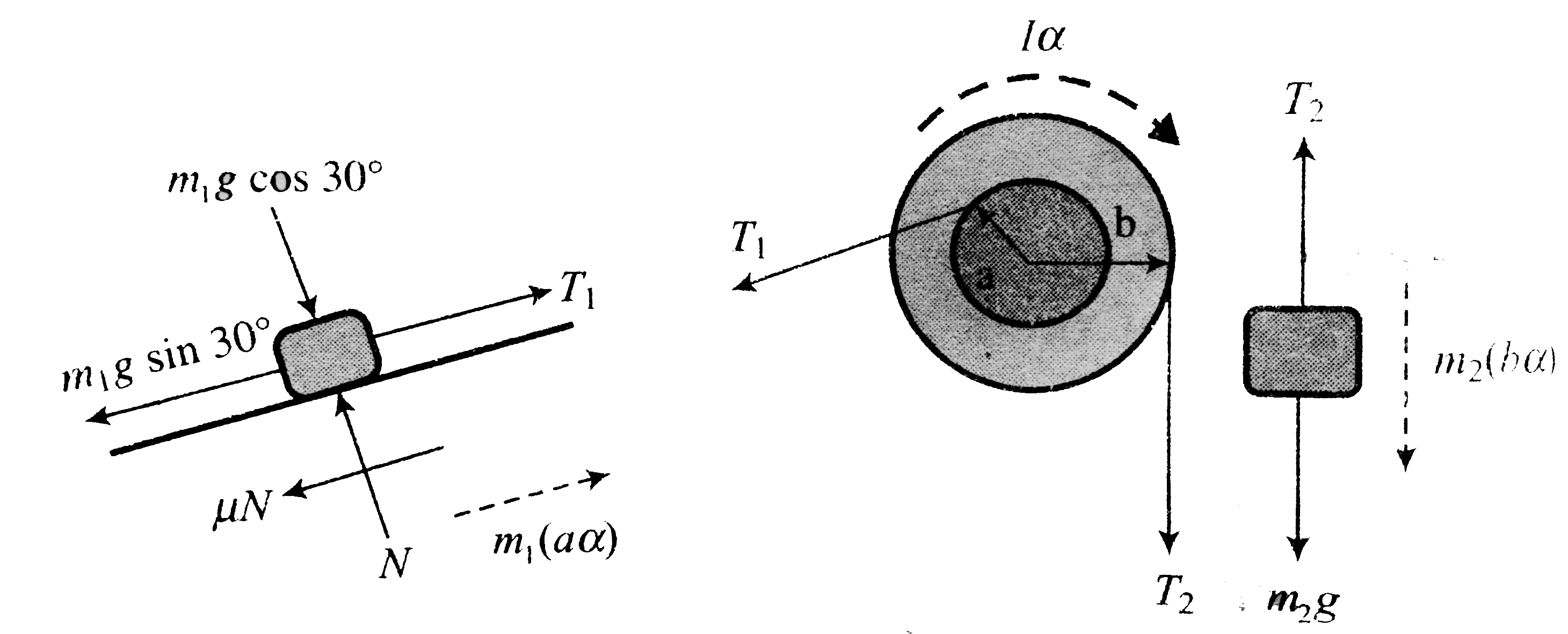
For forces on block A,N=m1gcos30∘ ...........i
T1−m1sin30i∘−μN=m1(aα).........ii
For forces on block B,m2g−T2=m2(bα)........iii
Taking moments of forces acting on pulley, about axis of rotation,
T1=17N,T2=26N and α−20rads−2
Acceleration of block A=aα=2ms−2 (up the plane)
Acceleration of block B=bα=3ms−2 (downward)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.217videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
The rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.
 09:29View Solution
09:29View SolutionTwo heavy particles having masses m1 and m2 are situated in a plane perpendicular to line AB at a distance or r1 and r2 respectively.

a. What is the moment of inertia of the system about axis AB?
b. What is the moment of inertia of the system about an axis passing through m1 and perpendicular to the line joining m1 and m2?
c. What is the moment of inertia of the system about an axis passing through m1 and m2?05:16View SolutionA solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.
 12:15View Solution
12:15View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
07:23View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO ot the nearest integer is
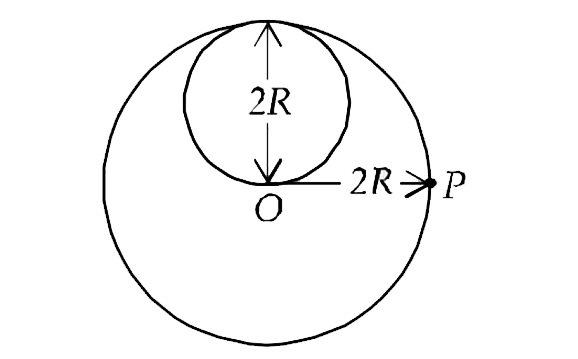 05:38View Solution
05:38View SolutionThe descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20 kg-m^2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.
 04:02View Solution
04:02View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
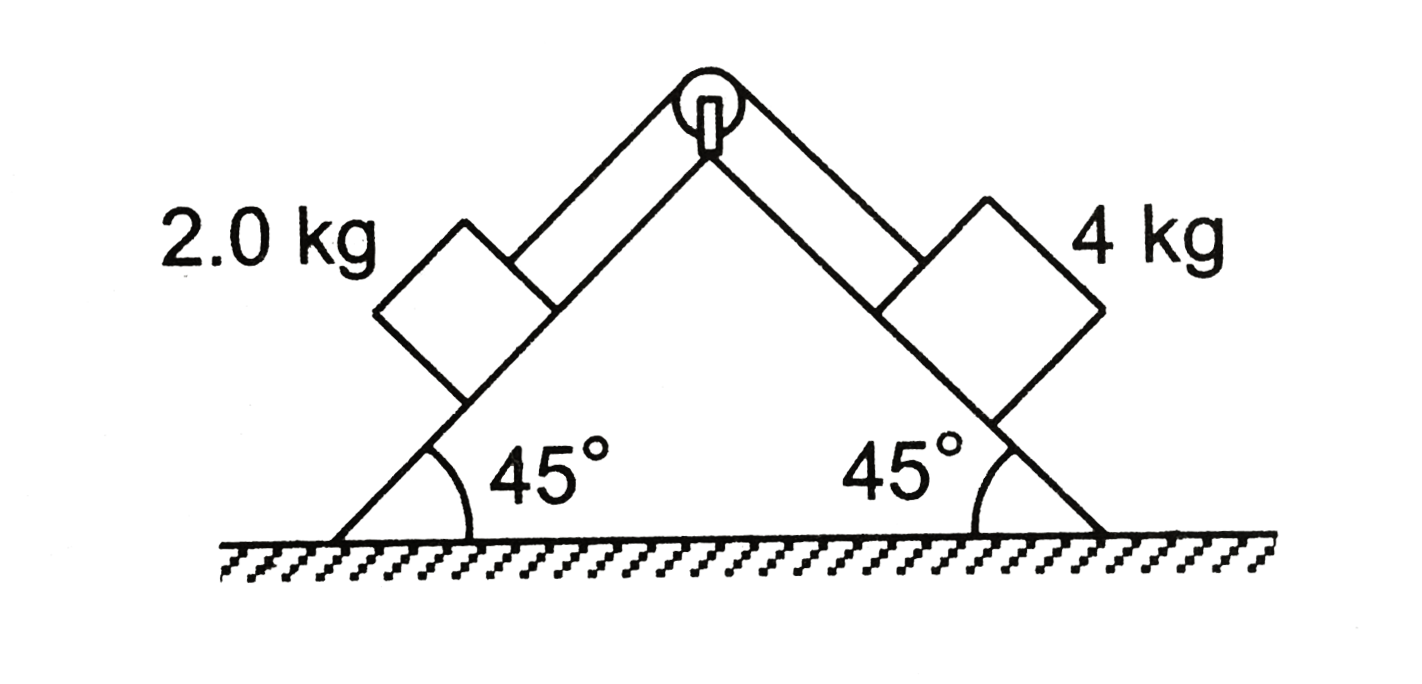 06:21View Solution
06:21View SolutionPulleys shown in the system are massless and fricionless. Threads are inextensible. The mass of blocks A, B, and C are m1=2kg,m2=4kg, and (m3)=2.75kg, respectively. Calculate the acceleration of each block.
 11:27View Solution
11:27View SolutionIn the arrangement shown in figure pulleys are mass of block A,b and C is m1=5kgm2=4kg and m3=2.5kg respectively .Co-efficient acceleration of friction for both the plane is μ=0.50 Calculate acceleration of which block when system is released from rest
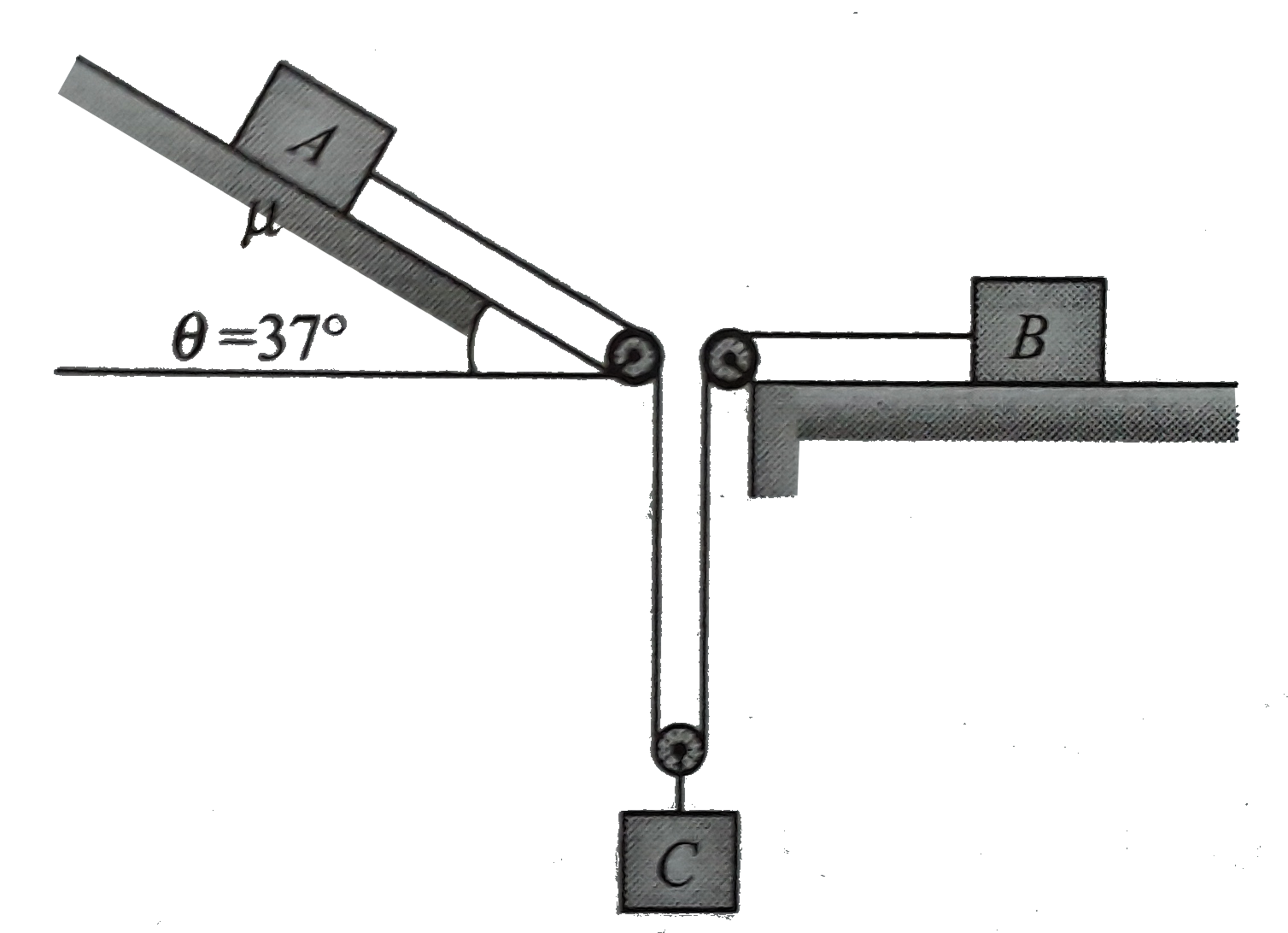 10:20View Solution
10:20View SolutionIn the system shown in figure mB=4kg , and mA=2kg . The pulleys are massless and friction is absent everywhere. The acceleration of block A is.
 07:58View Solution
07:58View SolutionIn the situation shown in figure F=500 newton applied on the pulley m_(1)=50 kg and m_(2) = 10 kg and pulley and strings are massless and frictionless. Then the acceleration of the pulley is : [g = 10 m//s^(2)]
06:41View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionPulleys shown in the system of the figure are massless and friction less. Threads are inextensible. Mass of block A, B and C are m1kg,m2=4kg and m3=2.75kg, respectively .Calculate acceleration of A block
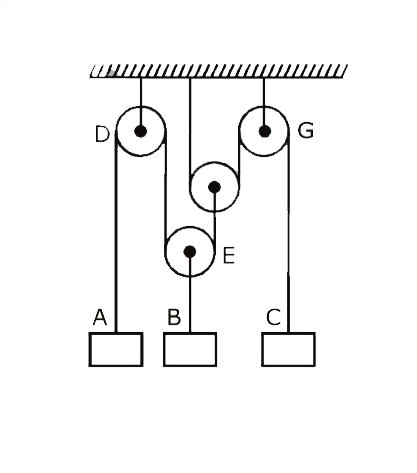 View Solution
View SolutionThe pulley as shown in the figure, consists of two discs of different diameters attached to the same shaft. The rope connected to the block of mass m_(1) = 1 kg passes over a smooth peg, while the block of mass m_(2) = 3 kg hangs vertically from one disc . The moment of inertia of the pulley is 0 . 2 kg m^(2), r_(1) = 5 cm and r_(2) = 10 cm . Find the tensions in the ropes and the accelerations of the blocks .
10:05View SolutionThe pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
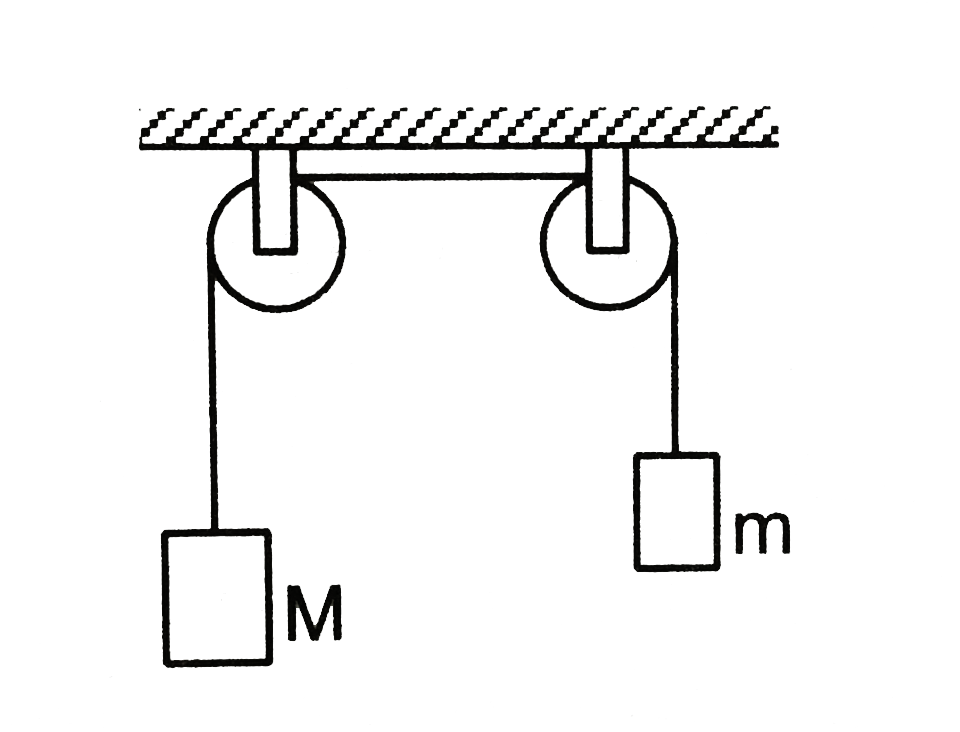 07:02View Solution
07:02View Solution

