Given below are observations on molar specific heats at room temperature of some common gases.
GasMolar specific heat (Cv)(cal mol1K−1)Hydrogen4.87Nitrogen4.97Oxygen5.02Nitric oxide4.99Carbon monoxide5.01Chlorine6.17
The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomie gas is2.52 cal/mol K. Explain this difference. What can you infer from the somewhat larger than the rest) value for chlorine ?
The gases are diatomic, and have other degrees of freedom fic, have other modes of motion) possible besides the translational degrees of freedom. To raise the temperature of the gas by a certain amount, heat is to be supplied to increase the average energy of all the modes Consequently, molar specific heat of diatomic gases is more than that of monatomie gases. It can be shown that if only rotational modes of motion are considered, the molar specific heat of diatomic gases is nearly (5/2) R which agrees with the observations for all the gases listed in the table, except chlorine. The higher value of molar specific heat of chlorine indicates that besides rotational modes, vibrational modes are also present in chlorine at room temperature.
Similar Questions
Given below are observations on molar specific heats at room temperature of some common gases
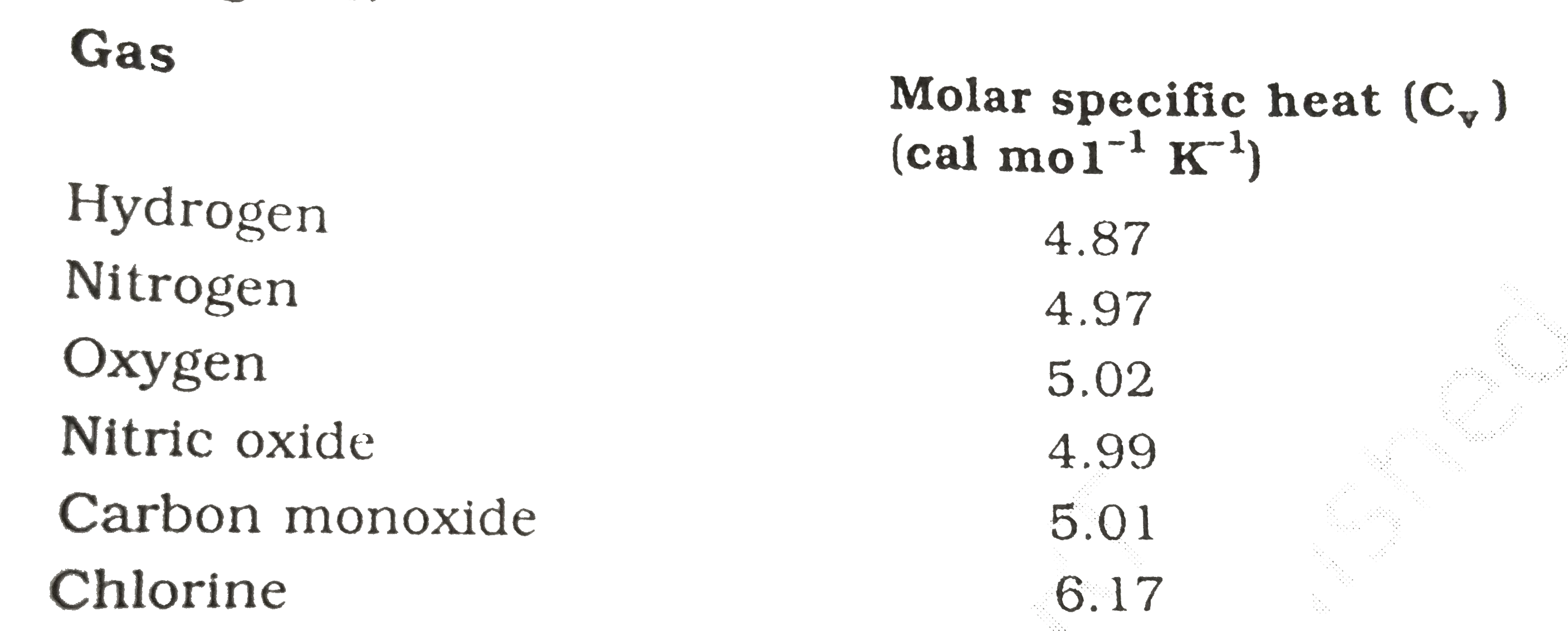
The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is 2.92 cal/mol K. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine ?
View SolutionGiven below are observations on molar specific heats at room temperature of some common gases
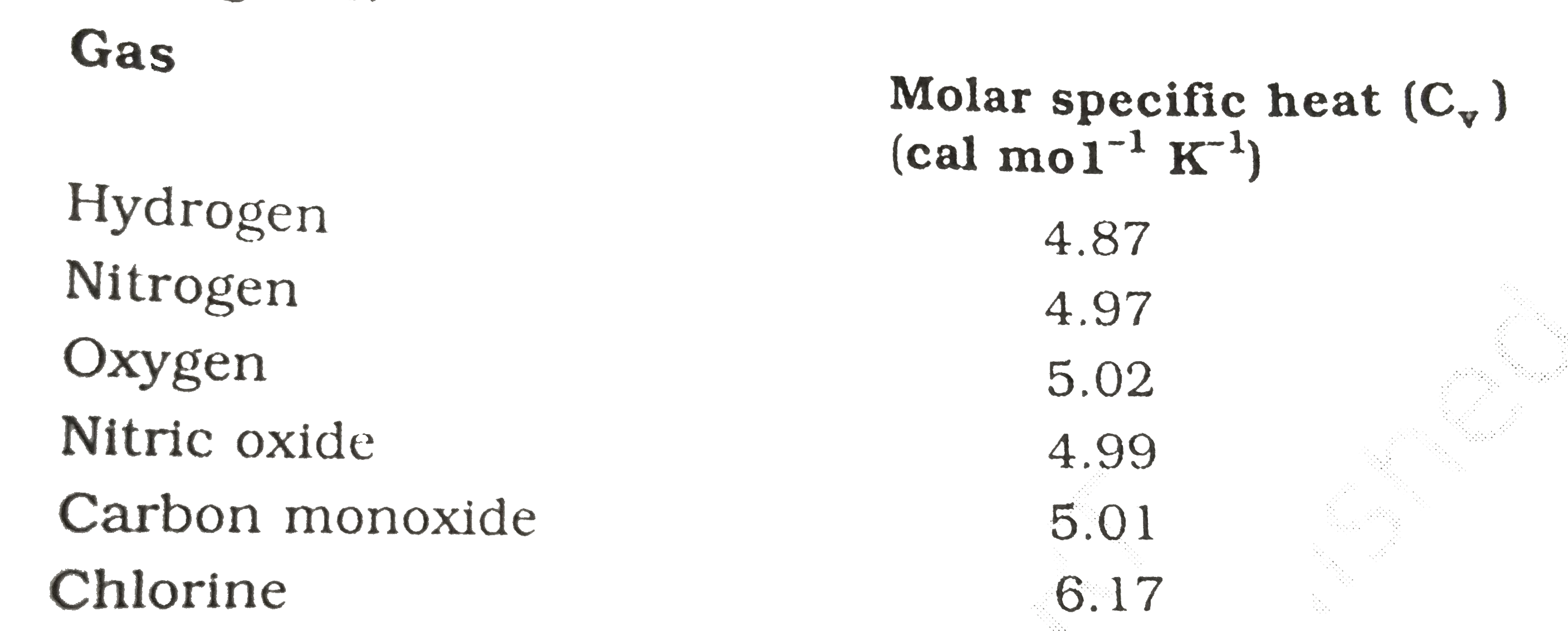
The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is 2.92 cal/mol K. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine ?
View Solution
Knowledge Check
Determine the quantity of heat added to 3.5 moles of the ideal gas argon if the temperature increases from 75∘C to 225∘C during an isobaric process .
(the molar specific of argon are Cv=3.0cal/Kmol and CP=5.0cal/Kmol)A2600 calB1600 calC21 00 calD1100 calMolar specific heat of oxygen at constant pressure is 7.2 cal/mol .∘C and R=8.3 J/mol K. at constant volume, 5 moles of oxygen is heated from 10∘C to 20∘C then the quantity of heat required will be
A25 calB50 calC260 calD500 cal
The molar specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root means square speed of the molecule of the gas at 120∘C. (1 cal = 4.2 J)
View SolutionThe molar specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root means square speed of the molecule of the gas at 120∘C. (1 cal = 4.2 J)
View SolutionCalculate the specific heat capacity at constant volume for a gas. Given specific heat capacity at constant pressure is 6.85calmol−1K−1,R=8.31Jmol−1K−1.
J−4.18Jcal−1.
View SolutionA vessel contains 0.5m3 of hydrogen gas at 300 K and pressure 105 Pa. How much heat should be added to it to raise the temperature to 500 K ? Molar specific heat of hydrogen is 5 cal/mol K:
View SolutionCalculate the value of mechanical equivalent of heat from the following data. Specific heat capacity of air at constant volume and at constant pressure are 4.93cal/mol−K and 6.90cal/mol−K respectively. Gas constant R=8.3J/mol−K.
View SolutionCalculate the value of mechanical equivalent of heat from the following data. Specific heat capacity of air at constant volume and at constant pressure are 4.93cal/mol−K and 6.90cal/mol−K respectively. Gas constant R=8.3J/mol−K.
View Solution
