Find the equation of the circle which touches both the axes and the line $x = c$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: ${(x - 1)}^{2} + {(y \pm 1)}^{2} = 1$

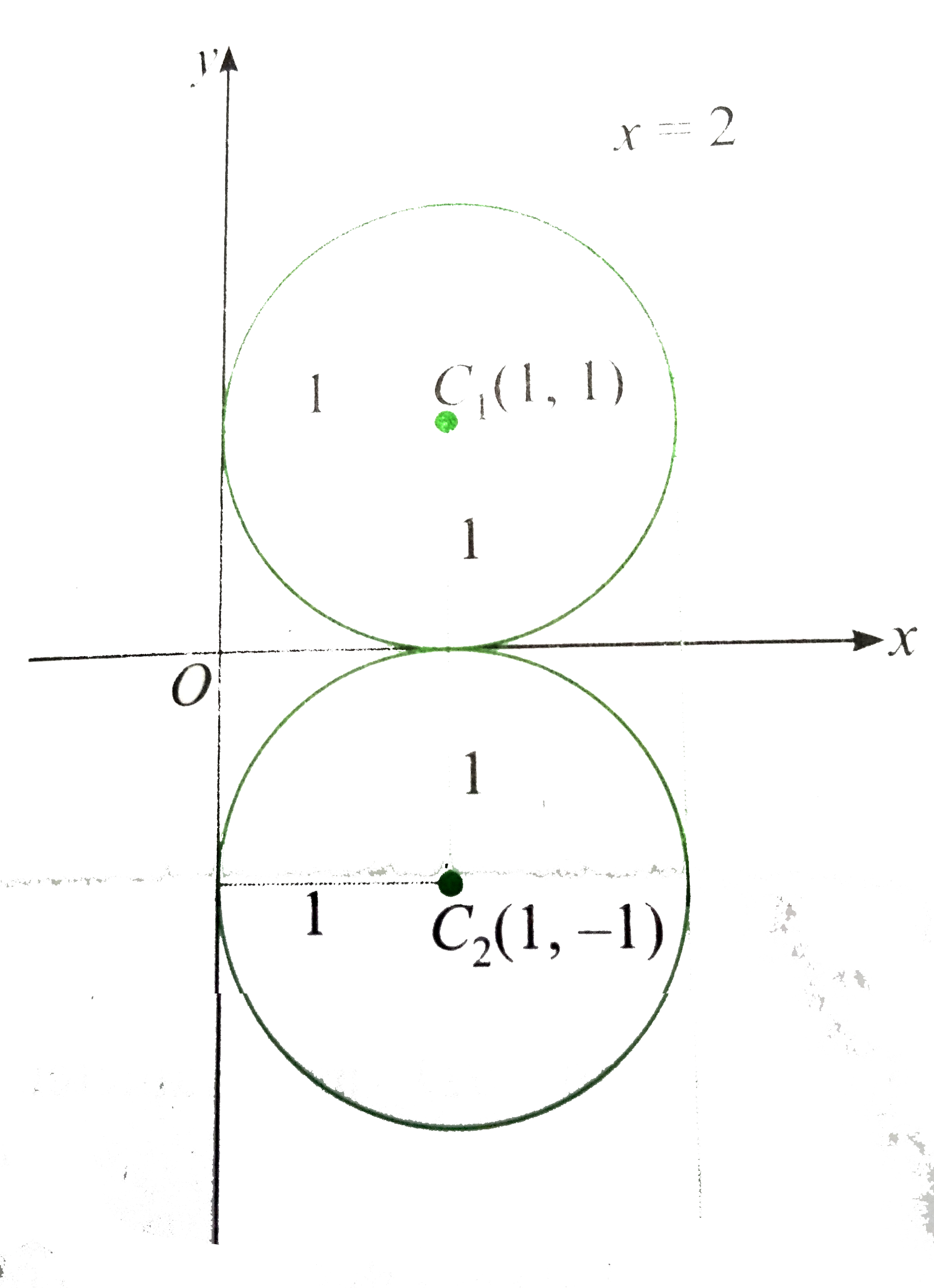
Clearly, radius of the circle is $' 1'$ and centre can be $(1, \pm 1)$
Therefore, equation of circle will be ${(x - 1)}^{2} + {(y \pm 1)}^{2} = 1$ .

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Find the equation of the circle which touches the x-axis and passes through the two points(1, -2) and (3, -4).
View Solution
Find the equation of the circle which touches both the axes and the line $3 x - 4 y + 8 = 0$ and lies in the third quadrant.
View Solution

Knowledge Check

Question 1 - Select One
The equations of the circles which touch both the axes and the line x = a are
A $x^{2} + y^{2} \pm c x \pm c y + \frac{c^{2}}{4} = 0$
B $x^{2} + y^{2} + c x \pm c y + \frac{c^{2}}{4} = 0$
C $x^{2} + y^{2} - c x \pm c y + \frac{c^{2}}{4} = 0$
Dnone of these
Question 2 - Select One
The equations of the circles which touch both the axes and the line x = a are
A $x^{2} + y^{2} \pm a x \pm a y + \frac{a^{2}}{4} = 0$
B $x^{2} + y^{2} + a x \pm a y + \frac{a^{2}}{4} = 0$
C $x^{2} + y^{2} - a x \pm a y + \frac{a^{2}}{4} = 0$
Dnone of these
Question 3 - Select One
Find the equation of a circle which touches both the axes and the line 3 4 8 0 x y - + = and lies in the third quadrant.
A $x^{2} + y^{2} + 4 x + 4 y - 4 = 0$
B $x^{2} + y^{2} - 4 x - 4 y + 4 = 0$
C $x^{2} + y^{2} + 4 x + 4 y + 4 = 0$
DNone of the above

CENGAGE-CIRCLE -Exercise 4.1

Home
Ask Doubt
Profile