A circle of radius 'r' passes through the origin O and cuts the axes at A and B,Locus of the centroid of triangle OAB is
x2+y2=(2k)2
x2+y2=(3k)2
x2+y2=(4k)2
x2+y2=(6k)2
The correct Answer is:1
Let the centroid of triangle OAB be (p,q).
Hence, points A and B are (3pm,0) and (0,3q), respectively.
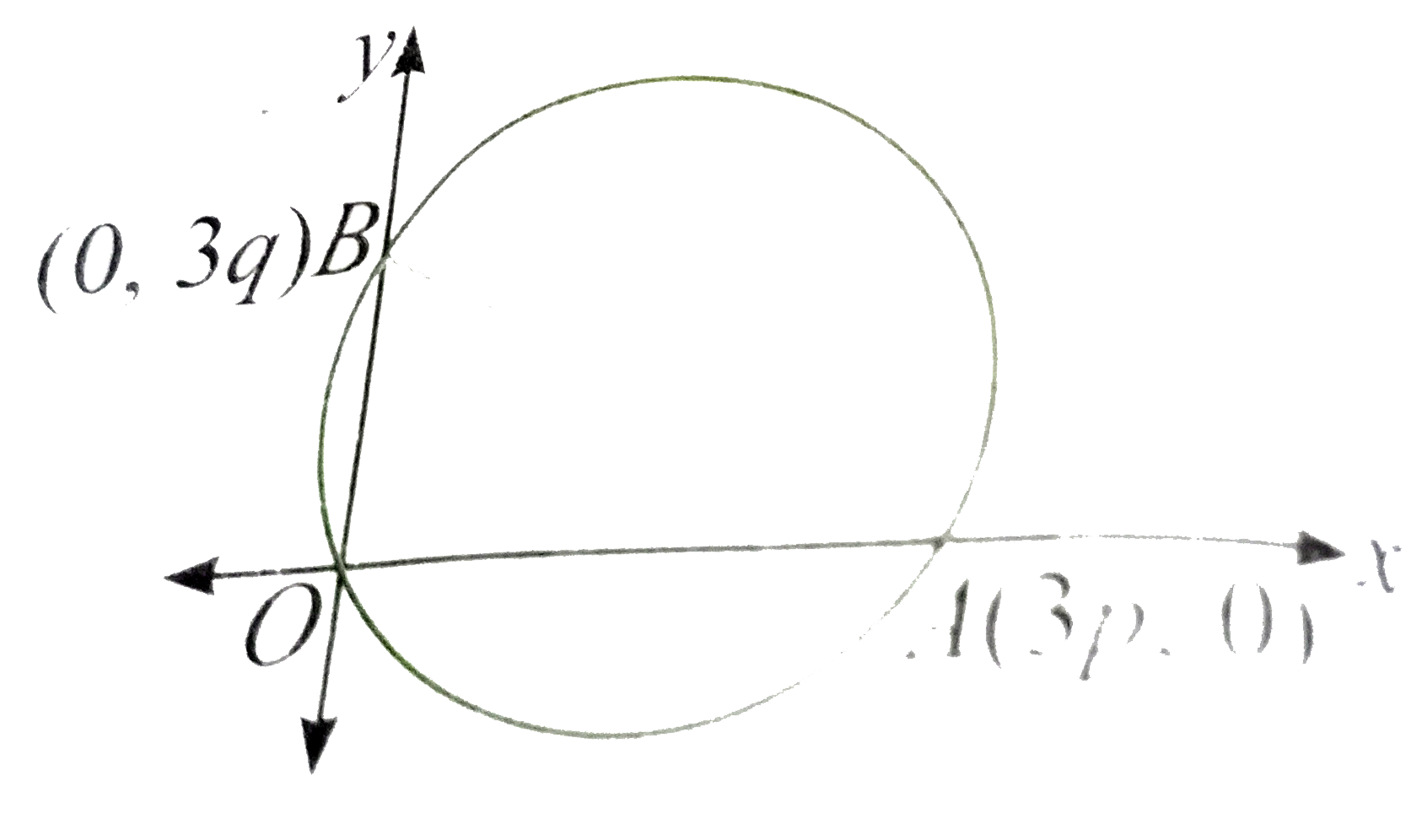
But diameter of circle, AB=6k
Hence, √9p2+9q2=6k
Therefore, the locus of (p,q) is x2+y2=4k2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
A circle of constant radius 2r passes through the origin and meets the axes in 'P' and 'Q' Locus of the centroid of the △POQ is :
Ax2+y2=r2B9(x2+y2)=16r2C2(x2+y2)=r2D3(x2+y2)=8r2A variable circle having fixed radius 'a' passes through origin and meets the co-ordinate axes in point A and B. Locus of centroid of triangle OAB where 'O' being the origin, is -
A9(x2+y2)=4a2B9(x2+y2)=a2C9(x2+y2)=2a2D9(x2+y2)=8a2A circle of constant radius r passes through the origin O, and cuts the axes at A and B. The locus of the foots the perpendicular from O to AB is (x2+y2)=4r2x2y2, Then the value of k is
A2B1C3D4
A sphere of constant radius k, passes through the origin and meets the axes at A,BandC. Prove that the centroid of triangle ABC lies on the sphere 9(x2+y2+z2)=4k2.
View SolutionA circle of radius r passes through the origin O and cuts the axes at AandB. Let P be the foot of the perpendicular from the origin to the line AB. Find the equation of the locus of P.
View SolutionA circle of constant radius r passes through the origin O and cuts the axes at A and B. Show that the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−2+y−2)=4r2.
View SolutionIf a sphere of constant radius k passes through the origin and meets the axis in A,B,C then the centroid of the triangle ABC lies on :
View SolutionA circle of constant radius 5 units passes through the origin O and cuts the axes at A and B. Then the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−1+y−2)=k then k=
View Solution
