From a point R(5, 8) two tangents RP and RQ are drawn to a given circle s=0 whose radius is 5. If circumcentre of the triangle PQR is (2, 3), then the equation of circle S = 0 is

A

$x^{2} + y^{2} + 2 x + 4 y - 20 = 0$

B

$x^{2} + y^{2} + x + 2 y - 10 = 0$

C

$x^{2} + y^{2} - x - 2 y - 20 = 0$

D

$x^{2} + y^{2} - 4 x - 6 y - 12 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

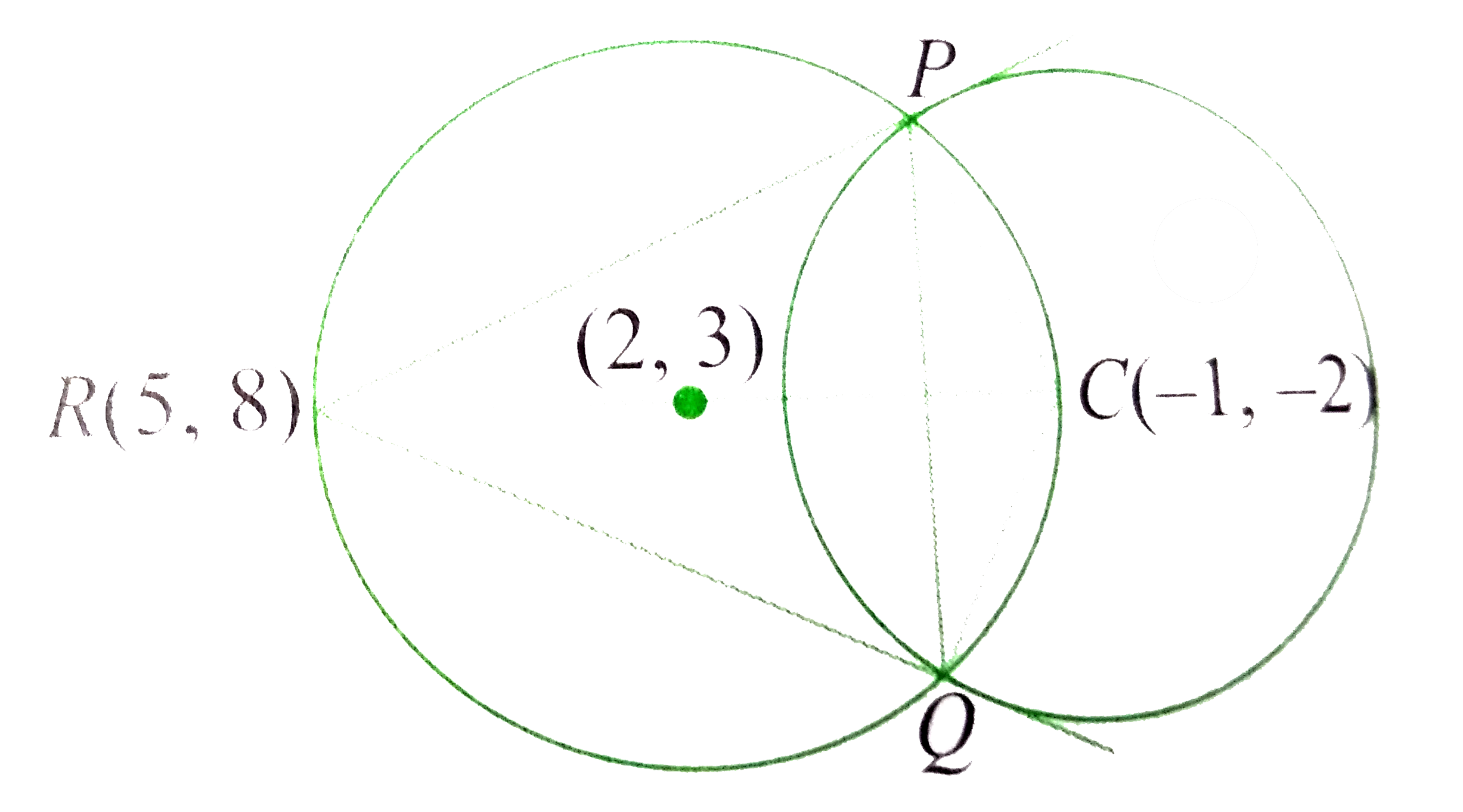
Let C be the center of the given circle.
Then, the circumcircle of $Δ R P Q$ passes through C.
Therefore, (2,3) is the midpoint of RC.
Thus, the coordinates of C are $(- 1, - 2)$ .
Hence, the equation of the circle is $x^{2} + y^{2} + 2 x + 4 y - 20 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a point P perpendicular tangents PQ and PR are drawn to ellipse $x^{2} + 4 y^{2} = 4$ , then locus of circumcentre of triangle PQR is
A $x^{2} + y^{2} = \frac{16}{5} {(x^{2} + 4 y^{2})}^{2}$
B $x^{2} + y^{2} = \frac{5}{16} {(x^{2} + 4 y^{2})}^{2}$
C $x^{2} + 4 y^{2} = \frac{16}{5} {(x^{2} + y^{2})}^{2}$
D $x^{2} + 4 y^{2} = \frac{16}{5} {(x^{2} + y^{2})}^{2}$
Question 2 - Select One
The length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
A3cm
B $4 \sqrt{2}$ cm
C $5 \sqrt{2} c m$
D $3 \sqrt{2}$ cm
Question 3 - Select One
If line $3 x + y = 0$ be a tangent to a circle drawn from origin to a circle centred at the point (2,- 1) then the equation of other tangent through the origin is
A $x - 3 y = 0$
B $x + 2 y = 0$
C $x + 3 y = 0$
D $3 x - y = 0$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile