The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
Which of the following does not change by changing the radius of the circle ?
Coordinartes of foci
Length of he major axis
Eccentricity
Length of the minor axis
Tangent at P(4cosθ,4sinθ)→x2+y2=16 is xcosθy+sinθ=4 (1)
The equation of AP is y=sinθcosθ−1(x−4) (2)
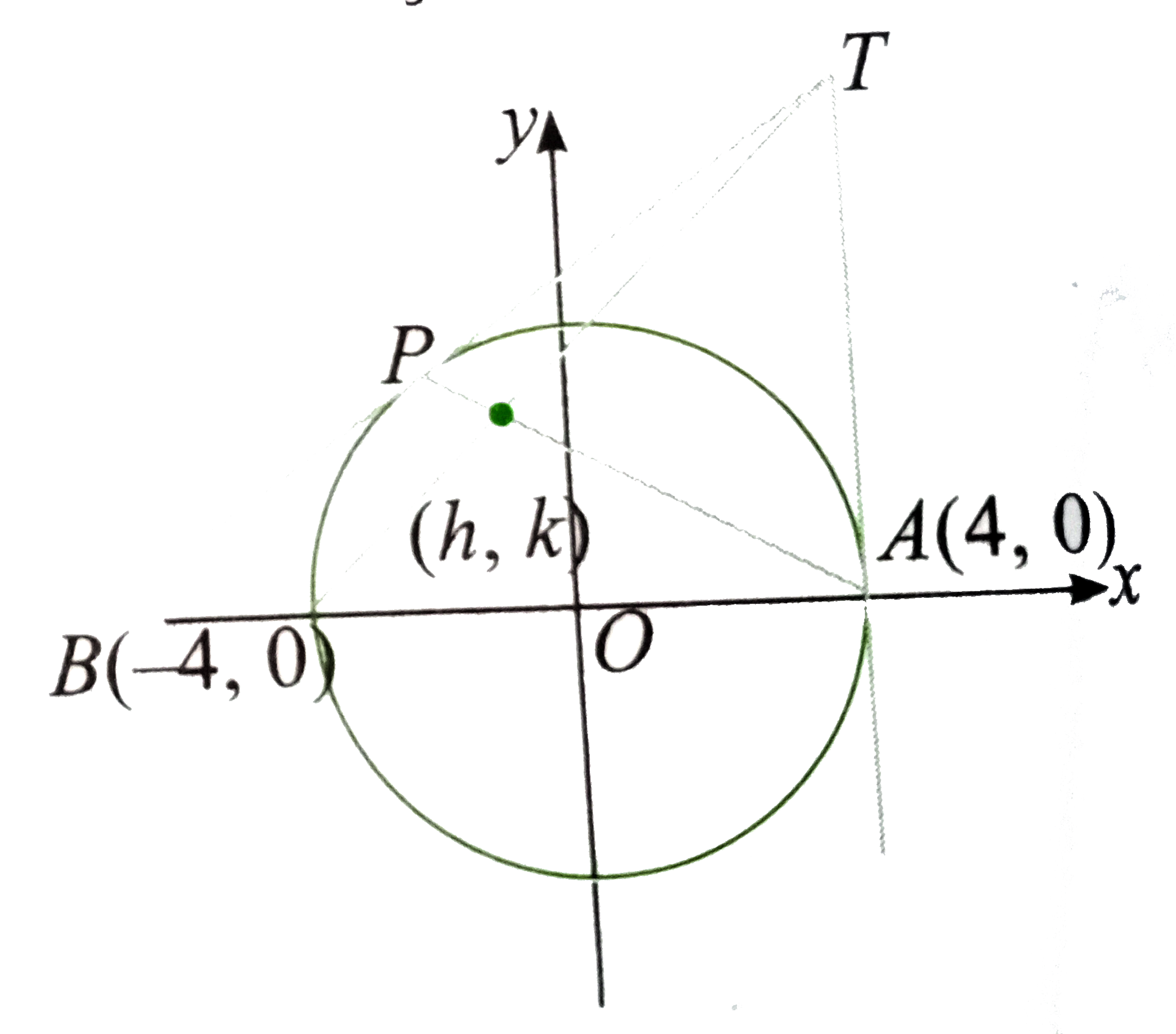
From (1), the coordinates of the point T are given by
(4,4(1−cosθ)sinθ)
The equation of BT is y=1−cosθ2sinθ(x+4) (3)
Let (h,k) be the point of intersection of the lines (2), and (3). Then we have
k2=−12(h2−16)
or h216+y28=1
Therefore, the locus of (h,k) is x216+y28=1
Which is an ellipse with eccehntrically e=1/√2
Sum of focal distance of any points is 2a=8
Considering the circle x2+y2=a2, we find the that the eccentricity of the ellipse is 1√2 which is contant and does not change by changing the radius of the circle
Similar Questions
The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The sum of focal distance of any point on the curce isView SolutionThe tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The locus of the intersection of AO and BT is a conic whosee eccentricity isView Solution
Knowledge Check
- Question 1 - Select One
The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The sum of focal distance of any point on the curce isA12B16C20D8 - Question 2 - Select One
The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The locus of the intersection of AO and BT is a conic whosee eccentricity isA1/2B1/√2C1/3D1/√3 - Question 3 - Select One
If tangent at any point P on the ellipse 7x2+16y2=12 cuts the tangent at the end points of the major axis at the points A and B, then the circle with AB as diameter passes through a fixed point whose coordinates are
A(±√a2−b2,0)B(±√a2+b2,0)C(0,±√a2−b2)D(0,√a2+b2)
The tangent at any point P of a circle x2+y2=a2 meets the tangent at a fixed point A(a,0) in T and T is joined to B, the other end of the diameter through A, prove that the locus of the intersection of AP and BT is an ellipse whose eccentricity is 1√2
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B.If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionA variable circle passes through the fixed point A(p, q) and touches x-axis. The locus of the other end of the diameter through A is:
View Solution

