किसी उत्तल गोलीय पृष्ठ पर प्रकाश के अपवर्तन के लिए सूत्र $\frac{n}{v} - \frac{1}{u} = \frac{n - 1}{R}$ स्थापित कीजिए | प्रतिको के सामान्य अर्थ है |

Video Solution

Text Solution

Verified by Experts

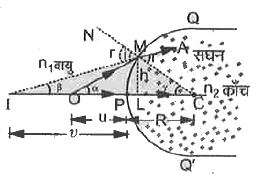
उत्तल गोलीय पृष्ठ पर अपवर्तन का सूत्र-माना QPQ. वक्रता त्रिज्या R का एक उत्तल गोलीय पृष्ठ है, जो निरपेक्ष अपवर्तनांक $n_{1}$ के विरल माध्यम को निरपेक्ष अपवर्तनांक $n_{2}$ के सघन माध्यम से पृथक करता है | इस पृष्ठ का ध्रुव P तथा वक्रता केंद्र C है | माना इसकी मुख्य अक्ष PC पर एक बिंदु-वस्तु O स्थित है, जिससे चलने वाली प्रकाश की एक किरण OM उत्तल पृष्ठ के बिंदु M पर आपतित होती है, जहाँ से वह दुसरे माध्यम में प्रवेश करती है | अभिलम्ब CMN की ओर झुक जाती है | दूसरी आपतित किरण OP गोइय पृष्ठ पर लम्बवत गिरती है और दुसरे माध्यम में सीधी चली जाती है | ये दोनों अपवर्तित किरणे पीछे की ओर बढाए जाने पर बिंदु I पर मिलती है , अत: बिंदु I, बिंदु-वस्तु O का आभासी प्रतिबिम्ब है |
मना आपतन कोण OMC=i, अपवर्तन कोण AMC=r, ध्रुव P से वस्तु की दुरी PO=-u, प्रतिबिम्ब की दुरी PI=-v तथा पृष्ठ की वक्रता त्रिज्या PC=+R है | माना OM, IM तथा CM मुख्य अक्ष से क्रमश: $α, β$ तथा $β$ कोण बनाती है तथा M से मुख्य अक्ष पर खींचे गए अभिलम्ब ML की ऊँचाई h है |
$Δ O M C$ में, $i = α + γ$ . . (1)
तथा $Δ I M C$ में, $r = β + γ$ . . (2)
स्नेल के नियमनुसार, $\frac{sin i}{sin r} = \frac{n_{2}}{n_{1}}$
यदि उत्तल गोलीय पृष्ठ का व्यास छोटा हो तो बिंदु M, ध्रुव P के निकट होगा, तब कोण $i$ व् r अत्यंत छोटे होंगे | यदि कोण $i$ व् r रेडियन में हो तो
$sin i = i$ तथा $sin r = r$
अत: $\frac{i}{r} = \frac{n_{2}}{n_{1}}$ अथवा $n_{1} i = n_{2} r$ . . (3)
समीकरण (1) व् समीकरण (2) से $i$ व् $r$ के मन समीकरण (3) में रखने पर,
$n_{1} (α + γ) = n_{2} (β + γ)$
अथवा $n_{1} α + n_{1} γ = n_{2} β + n_{2} γ$
अथवा $- n_{2} β + n_{1} α = γ (n_{2} - n_{1})$ . . (4)
चूँकि पृष्ठ का छोटा माना गया है, अत: कोण $α, β$ व् $γ$ भी छोटे होंगे तथा बिंदु M व् L ध्रुव P के समीप होगे| इस दशा में,
$α = tan α = \frac{M L}{L O} = \frac{M L}{P O} = \frac{h}{(- u)}$
$β = tan β = \frac{M L}{L I} = \frac{M L}{P I} = \frac{h}{(- v)}$
$γ = tan γ = \frac{M L}{L C} = \frac{M L}{P C} = \frac{h}{R}$
$α, β$ व् $γ$ के मान समीकरण (4) में रखने पर,
$- n_{2} (\frac{h}{- v}) + n_{1} (\frac{h}{- u}) = (n_{2} - n_{1}) \frac{h}{R}$
अथवा $\frac{n_{2}}{v} - \frac{n_{1}}{u} = \frac{(n_{2} - n_{1})}{R}$ . . (5)
यदि n विरल माध्यम के सापेक्ष का अपवर्तनांक है तो $n_{2} / n_{1} = n,$ अत: समीकरण (5) से,
$\frac{n_{2} / n_{1}}{v} - \frac{1}{u} = \frac{(n_{2} / n_{1} - 1)}{R}$
अथवा $\frac{n}{v} - \frac{1}{u} = \frac{n - 1}{R}$
इस सूत्र के अनुसार v का मान $α$ पर निर्भर नही करता, अत: बिंदु वस्तु O से चलने वाली सभी किरणे उत्तल पृष्ठ से अपवर्तित होकर एक ही बिंदु I से आती हुई प्रतीत होंगी अर्थात I, O का आभासी प्रतिबिम्ब है |

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

UP BOARD PREVIOUS YEAR-किरण प्रकाशिकी एवं प्रकाशिकी यन्त्र-बहुविकल्पीय प्रश्नोत्तर

Home
Ask Doubt
Profile