यंग के दो स्लिटों के प्रयोग में किसी दीप्त फ्रिज की केन्द्रीय फ्रिज से दूरी के लिए व्यंजक प्राप्त कीजिए तथा इसकी सहायता से फ्रिन्ज-चौड़ाई का मान ज्ञात कीजिए।
अथवा प्रकाश के व्यतिकरण सम्बन्धी यंग के प्रयोग का सिद्धान्त स्पष्ट करते हुए फ्रिन्ज की चौड़ाई के लिए सूत्र W=Dλ/d की स्थापना कीजिए।
अथवा यंग के द्वि-स्लिट प्रयोग में प्राप्त व्यतिकरण फ्रिन्जों की चौड़ाई हेतु व्यंजक प्राप्त कीजिए।
अथवा स्लिटों के बीच की दूरीd, स्लिटों व स्क्रीन के बीच की दूरी D तथा प्रयुक्त प्रकाश की तरंगदैर्घ्य है।
अथवा प्रकाश के व्यतिकरण सम्बन्धी यंग के प्रयोग के सिद्धान्त को समझाइए। फ्रिज चौड़ाई के लिए सूत्र स्थापित कीजिए।
अथवा कला सम्बद्ध स्रोत से क्या समझते हैं? स्थैतिक व्यतिकरण पैटर्न प्राप्त करने के लिए आवश्यक प्रतिबन्धों को लिखिए। दिखाइए कि यंग के द्विक रेखाछिद्र प्रयोग में दीप्त तथा अदीप्त फ्रिन्जों की चौड़ाई समान होती है।
अथवा यंग के व्यतिकरण प्रयोग में, दो समान्तर स्लिटों के बीच की दूरीd और स्लिटों से पर्दे की दूरी D है। यदि प्रकाश की तरंगदैर्घ्य । हो, तो पर्दे पर एक दीप्त फ्रिज के लिए केन्द्रीय फ्रिन्ज से दूरी के लिए व्यंजक प्राप्त कीजिए।
अथवा यंग के द्विक रेखा छिद्र के प्रयोग की सहायता से फ्रिन्ज की चौड़ाई का व्यंजक प्राप्त कीजिए।
Video Solution
Text Solution
कला सम्बद्ध स्रोत–(लघु उत्तरीय प्रश्नोत्तर I का प्रश्न 7 देखें।) स्थैतिक व्यतिकरण पैटर्न प्राप्त करने के लिए आवश्यक प्रतिबन्ध(लघु उत्तरीय प्रश्नोत्तर I का प्रश्न 6 देखें)
व्यतिकरण सम्बन्धी यंग का प्रयोग–यंग ने एकवर्णी प्रकाश के समतल तरंगाग्र को एक पर्दे P में बने रेखाछिद्र पर डाला। रेखाछिद्र S एकवणी प्रकाश स्रोत की भाँति कार्य करता है। पर्दे P से कुछ दूरी पर रखे एक अन्य पर्दे Q में S से समान दूरी पर दो रेखाछिद्र S1 व S2 बनाए। प्रकाश स्रोत S से चलने वाली द्वितीयक तरंगिकाएँ S1 S2 पर समान कला में पहुंचती हैं। अब S1S2 भी तरंग स्रोत की भाँति कार्य करते हैं और इनसे चलने वाली तरंगिकाएँ परस्पर अध्यारोपित होकर D दूरी पर स्थित पर्दे पर व्यतिकरण फ्रिन्ज बनाती है। जिन
स्थानों पर ये तरंगिकाएँ समान कला में मिलती हैं, उन स्थानों पर संपोषी व्यतिकरण के कारण दीप्ति फ्रिन्ज प्राप्त होती हैं जबकि जिन स्थानों पर तरंगिकाएँ विपरीत कला में मिलती हैं, उन स्थानों पर विनाशी व्यतिकरण के कारण अदीप्त फ्रिन्ज प्राप्त होती हैं।
फ्रिज की चौड़ाई के लिए व्यंजक-माना S एक रेखाछिद्र है, जिसे एकवर्णी प्रकाश से प्रकाशित किया गया है। इस रेखाछिद्र से आगे दो रेखाछिद्र S1वS2हैं, जो एक-दूसरे के बहुत समीप हैं, 8 के समान्तर है तथा उससे समान दूरी पर स्थित हैं। से चलने वाली द्वितीयक तरंगिकाएँ S1S2 पर समान कला में पहुँचती हैं। हाइगेन्स के सिद्धान्तानुसार, S1 व S2 भी द्वितीयक तरंगिकाओं के स्रोत बन जाते हैं। ये तरंगिकाएँ परस्पर अध्यारोपण करती हुई D दूरी पर स्थित पर्दे पर व्यतिकरण फ्रिन्जे बनाती हैं।

माना पदें के बिन्दु P पर दीप्त फ्रिन्ज बनती है। माना द्विक रेखाछिद्र S1S2 का लम्बार्द्धक CO,पदें से बिन्दु O पर मिलता है तथा बिन्दु P की O से दूरी x है। अतः
रेखाछिद्रों S1 व S2 से बिन्दु P पर पहुंचने वाली तरंगिकाओं के बीच पथान्तर =S2P−S1P
माना S1 से S2P पर लम्ब S1A डाला गया है। अतः बिन्दु P पर दोनों तरंगों के बीच पथान्तर (S2P−S1P)=S2A
△S1S2A तथा △PCO समरूप त्रिभुज हैं।
S2AS1S2=OPCPअथवा S2AS1S2=OPCO
यदि S1S2=d है, तब S2Ad=XD
अतः पथान्तर S2A=XdD
केन्द्रीय फ्रिन्ज से दीप्त फ्रिन्ज की दूरी का व्यंजक-यदि प्रकाश तरंगिकाओं को पथान्तर 0,lambda,2lambda,...... है तो प्रकाश की तीव्रता अधिकतम होगी।
अतः दीप्त फ्रिन्जों (अधिकतम तीव्रता) के लिए
XdD=mλ [जहाँ m = 0, 1, 2, ......]
अत: mवीं अदीप्त फ्रिज की बिन्दु O से दूरी X=mDλd
इस सूत्र में m= 0 रखने पर, केन्द्रीय दीप्त फ्रिन्ज (अथवा शून्य क्रम फ्रिन्ज) m=1 रखने पर, पहली दीप्त फ्रिन्ज तथा m = 2रखने पर, दूसरी दीप्त फ्रिन्ज की स्थिति...... आदि प्राप्त होती है।
केन्द्रीय फ्रिन्ज से अदीप्त फ्रिन्ज की दूरी का व्यंजक-यदि प्रकाश तरंगिकाओं का पथान्तर λ/2,3λ/2,5λ/2,....... है, तो प्रकाश की तीव्रता न्यूनतम होगी।
अत: अदीप्त फ्रिन्जों (न्यूनतम तीव्रता) के लिए XdD=(m−12)λ[जहाँ m = 0, 1, 2,...]
अत: mवीं अदीप्त फ्रिन्ज की बिन्दु Oसे दूरी
X=(m−12)Dλd=(2m−1)Dλ2d
इस सूत्र में m = 1 रखने पर, पहली अदीप्त फ्रिन्ज तथा m= 2 रखने पर, दूसरी अदीप्त फ्रिन्ज की स्थिति ....... आदि प्राप्त होती है।
फ्रिन्जों की चौड़ाई-यदि mवीं और (m + 1) वीं दीप्त फ्रिन्जों की केन्द्रीय फ्रिन्ज से दूरियाँ क्रमश: Xm तथा Xm+1 हो तो
Xm=mDλd तथा Xm+1=(m+1)Dλd
अत: mवीं तथा (m + 1) वीं दीप्त फ्रिन्जों के बीच की दूरी
W=Xm+1−Xm
=(m+1)Dλd−mDλd=Dλd
इसी प्रकार mवीं तथा (m+ 1)वीं दीप्त फ्रिन्जों के बीच की दूरीW=X.(m+1)−X.m
=[2(m+1)−1]Dλ2d−(2m−1)DA2d=Dλd
इस प्रकार दीप्त तथा अदीप्त फ्रिन्जों की चौड़ाई समान होती है। ... व्यतिकरण फ्रिन्ज की चौड़ाईW=Dλd

|
Similar Questions
यंग का द्वि स्लिट प्रयोग
View Solutionयंग का द्वि- स्लिट प्रयोग#!#यंग का एकल झिरी प्रयोग
View Solutionगरुभूमि के इलाके में वर्षा की मात्रा नापने के लिए किस इकाई.का प्रयोग होता है?
View Solutionव्यतिकरण #!#यंग का द्वि स्लिट प्रयोग
View Solutionवायु के आधिक्य में सोडियम के दहन से एक उच्च ऑक्साइड प्राप्त होता है । उत्पाद में ऑक्सीजन की ऑक्सीकरण अवस्था क्या है ? ऋणात्मक चिन्ह की उपेक्षा कीजिए ।
View Solutionसमान विभवांतर के माध्यम से त्वरित हुए alpha कण और प्रोटॉन के लिए तरंग दैर्ध्य के अनुपात की गणना कीजिए।
View Solutionनिम्न के लिए हाइड्रोजनीकरण की ऊष्मा की तुलना कीजिए-
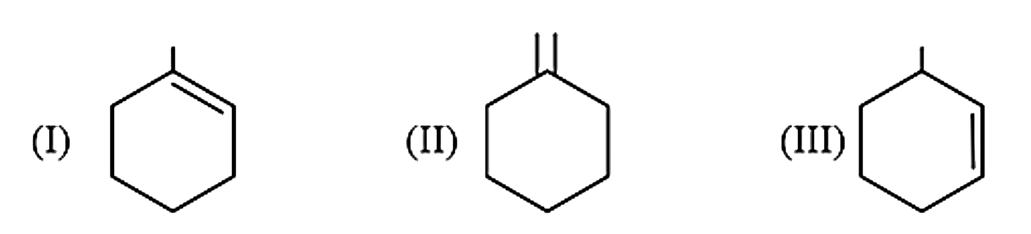
View SolutionRevision|मेंडल के नियम |मेंडल के नियम अथवा वंशागति के सिद्धांत |मेंडल का एकल संकरण प्रयोग तथा द्विसंकरण प्रयोग |प्रभावित का नियम |युग्मकों की शुद्धता का नियम |OMR
View Solution
